7  Instrumental Variables

Causal Inference:
The Mixtape.

Buy the print version today:

Buy from Amazon Buy from Yale Press

\[ % Define terms \newcommand{\Card}{\text{Card }} \DeclareMathOperator*{\cov}{cov} \DeclareMathOperator*{\var}{var} \DeclareMathOperator{\Var}{Var\,} \DeclareMathOperator{\Cov}{Cov\,} \DeclareMathOperator{\Prob}{Prob} \newcommand{\independent}{\perp \!\!\! \perp} \DeclareMathOperator{\Post}{Post} \DeclareMathOperator{\Pre}{Pre} \DeclareMathOperator{\Mid}{\,\vert\,} \DeclareMathOperator{\post}{post} \DeclareMathOperator{\pre}{pre} \]

Just as Archimedes said, “Give me a fulcrum, and I shall move the world,” you could just as easily say that with a good-enough instrument, you can identify any causal effect. But, while that is hyperbole, for reasons we will soon see, it is nonetheless the case that the instrumental variables (IV) design is potentially one of most important research designs ever devised. It is also unique because it is one of those instances that the econometric estimator was not simply ripped off from statistics (e.g., Eicker-Huber-White standard errors) or imported from some other field (e.g., like regression discontinuity). IV was invented by an economist, and its history is fascinating.

7.1 History of Instrumental Variables: Father and Son

Philip Wright was born in 1861 and died in 1934. He received his bachelor’s degree from Tufts in 1884 and a master’s degree from Harvard in 1887. His son, Sewall Wright, was born in 1889 when Philip was 28. The family moved from Massachusetts to Galesburg, Illinois, where Philip took a position as professor of mathematics and economics at Lombard College. Philip published numerous articles and books in economics over his career, and he published poetry, too. You can see his vita here at https://scholar.harvard.edu/files/stock/files/wright_cv.jpg.¹ Sewall attended Lombard College and took his college mathematics courses from his father.

In 1913, Philip took a position at Harvard, and Sewall entered there as a graduate student. Philip would later leave for the Brookings Institute, and Sewall would take his first job in the Department of Zoology at the University of Chicago, where he would eventually be promoted to professor in 1930.

Philip was prolific, which, given his sizable teaching and service requirements, is impressive. He published in top journals such as Quarterly Journal of Economics, Journal of the American Statistical Association, Journal of Political Economy, and American Economic Review. A common theme across many of his publications was the identification problem. He was acutely aware of it and intent on solving it.

In 1928, Philip was writing a book about animal and vegetable oils. The reason? He believed that recent tariff increases were harming international relations. And he wrote about the damage from the tariffs, which had affected animal and vegetable oils. The book, it turns out, would become a classic—not for tariffs or oils, but for being the first proof for the existence of an instrumental variables estimator.

While his father was publishing like a fiend in economics, Sewall Wright was revolutionizing the field of genetics. He invented path analysis, a precursor to Pearl’s directed acyclical graphic models, and he made important contributions to the theory of evolution and genetics. He was a genius. The decision to not follow in the family business (economics) created a bit of tension between the two men, but all evidence suggests that they found each other intellectually stimulating.

In his book on vegetable and oil tariffs, there is an appendix (entitled Appendix B) in which the calculus of an instrumental variables estimator was worked out. Elsewhere, Philip thanked his son for his valuable contributions to what he had written, referring to the path analysis that Sewall had taught him. This path analysis, it turned out, played a key role in Appendix B.

Appendix B showed a solution to the identification problem. So long as the economist is willing to impose some restrictions on the problem, then the system of equations can be identified. Specifically, if there is one instrument for supply, and the supply and demand errors are uncorrelated, then the elasticity of demand can be identified.

But who wrote this Appendix B? Either man could’ve done so. It is a chapter in an economics book, which points to Philip. But it used the path analysis, which points to Sewall. Historians have debated this, even going so far as to accuse Philip of stealing the idea from his son. If Philip stole the idea, by which I mean that when he published Appendix B, he failed to give proper attribution to his son, then it would at the very least have been a strange oversight. In come Stock and Trebbi (2003) to offer their opinions to this debate over authorship.

Stock and Trebbi (2003) tried to determine the authorship of Appendix B using “stylometric analysis.” Stylometric analysis had been used in other applications, such as to identify the author of the 1996 political novel Primary Colors (Joseph Klein) and the unsigned Federalist Papers. But Stock and Trebbi (2003) is easily the best application of stylometric analysis in economics.²

The method is akin to contemporary machine learning methods. The authors collected raw data containing the known original academic writings of each man, plus the first chapter and Appendix B of the book in question. All footnotes, graphs, and figures were excluded. Blocks of 1,000 words were selected from the files. Fifty-four blocks were selected: twenty written by Sewall with certainty, twenty-five by Philip, six from Appendix B, and three from chapter 1. Chapter 1 has always been attributed to Philip, but Stock and Trebbi (2003) treat the three blocks as unknown to check whether their model is correctly predicting authorship when authorship is already known.

The stylometric indicators that they used included the frequency of occurrence in each block of 70 function words. The list was taken from a separate study. These 70 function words produced 70 numerical variables, each of which is a count, per 1,000 words, of an individual function word in the block. Some words were dropped (e.g., “things” because they occurred only once), leaving 69 function words.

The second set of stylometric indicators, taken from another study, concerned grammatical constructions. Stock and Trebbi (2003) used 18 grammatical constructions, which were frequency counts. They included things like noun followed by an adverb, total occurrences of prepositions, coordinating conjunction followed by noun, and so on. There was one dependent variable in their analysis, and that was authorship. The independent variables were 87 covariates (69 function word counts and 18 grammatical statistics).

The results of this analysis are absolutely fascinating. For instance, many covariates have very large \(t\)-statistics, which would be unlikely if there really were no stylistic differences between the authors and the indicators were independently distributed.

So what do they find? Most interesting is their regression analysis. They write:

We regressed authorship against an intercept, the first two principal components of the grammatical statistics and the first two principal components of the function word counts, and we attribute authorship depending on whether the predicted value is greater or less than 0.5. (p.191)

And what did they find? That all of the Appendix B and chapter 1 blocks were assigned to Philip, not Sewall. They did other robustness checks, and all of them still pointed to Philip as the author.

Writing Appendix B and solving the problem that became Appendix B are technically distinct. But I nonetheless love this story for many reasons. First, I love the idea that an econometric estimator as important as instrumental variables has its roots in economics. I’m so accustomed to stories in which the actual econometric estimator was lifted from statistics (Huber-White standard errors) or educational psychology (regression discontinuity) that it’s nice to know economists have added their own designs to the canon. But the other part of the story that I love is the father-son component. It’s encouraging to know that a father and son can overcome differences through intellectual collaborations such as this. Such relationships are important, and tensions, when they arise, should be vigorously pursued until those tensions dissolve if possible. Relationships, and love more generally, matter after all. And Philip and Sewall give a story of that.

7.2 Intuition of Instrumental Variables

7.2.1 Canonical IV DAG

To understand the instrumental variables estimator, it is helpful to start with a DAG that shows a chain of causal effects that contains all the information needed to understand the instrumental variables strategy. First, notice the backdoor path between \(D\) and \(Y\): \(D \leftarrow U \rightarrow Y\). Furthermore, note that \(U\) is unobserved by the econometrician, which causes the backdoor path to remain open. If we have this kind of selection on unobservables, then there does not exist a conditioning strategy that will satisfy the backdoor criterion (in our data). But, before we throw up our arms, let’s look at how \(Z\) operates through these pathways.

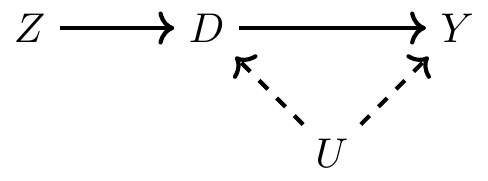
First, there is a mediated pathway from \(Z\) to \(Y\) via \(D\). When \(Z\) varies, \(D\) varies, which causes \(Y\) to change. But, even though \(Y\) is varying when \(Z\) varies, notice that \(Y\) is only varying because \(D\) has varied. You sometimes hear people describe this as the “only through” assumption. That is, \(Z\) affects \(Y\) “only through” \(D\).

Imagine this for a moment though. Imagine \(D\) consists of people making choices. Sometimes these choices affect \(Y\), and sometimes these choices are merely correlated with changes in \(Y\) due to unobserved changes in \(U\). But along comes some shock, \(Z\), which induces some but not all of the people in \(D\) to make different decisions. What will happen?

Well, for one, when those people’s decisions change, \(Y\) will change too, because of the causal effect. But all of the correlation between \(D\) and \(Y\) in that situation will reflect the causal effect. The reason is that \(D\) is a collider along the backdoor path between \(Z\) and \(Y\).

But I’m not done with this metaphor. Let’s assume that in this \(D\) variable, with all these people, only some of the people change their behavior because of \(D\). What then? Well, in that situation, \(Z\) is causing a change in \(Y\) for just a subset of the population. If the instrument only changes the behavior of women, for instance, then the causal effect of \(D\) on \(Y\) will only reflect the causal effect of women’s choices, not men’s choices.

There are two ideas inherent in the previous paragraph that I want to emphasize. First, if there are heterogeneous treatment effects (e.g., men affect \(Y\) differently than women do), then our \(Z\) shock only identified some of the causal effect of \(D\) on \(Y\). And that piece of the causal effect may only be valid for the population of women whose behavior changed in response to \(Z\); it may not be reflective of how men’s behavior would affect \(Y\). And second, if \(Z\) is inducing some of the change in \(Y\) via only a fraction of the change in \(D\), then it’s almost as though we have less data to identify that causal effect than we really have.

Here we see two of the difficulties in interpreting instrumental variables and identifying a parameter using instrumental variables. Instrumental variables only identify a causal effect for any group of units whose behaviors are changed as a result of the instrument. We call this the causal effect of the complier population; in our example, only women “complied” with the instrument, so we only know its effect for them. And second, instrumental variables are typically going to have larger standard errors, and as such, they will fail to reject in many instances if for no other reason than being underpowered.

Moving along, let’s return to the DAG. Notice that we drew the DAG such that \(Z\) is independent of \(U\). You can see this because \(D\) is a collider along the \(Z \rightarrow D \leftarrow U\) path, which implies that \(Z\) and \(U\) are independent. This is called the “exclusion restriction,” which we will discuss in more detail later. But briefly, the IV estimator assumes that \(Z\) is independent of the variables that determine \(Y\) except for \(D\).

Second, \(Z\) is correlated with \(D\), and because of its correlation with \(D\) (and \(D\)’s effect on \(Y\)), \(Z\) is correlated with \(Y\) but only through its effect on \(D\). This relationship between \(Z\) and \(D\) is called the “first stage” because of the two-stage least squares estimator, which is a kind of IV estimator. The reason it is only correlated with \(Y\) via \(D\) is because \(D\) is a collider along the path \(Z\rightarrow D \leftarrow U \rightarrow Y\).

7.2.2 Good instruments should feel weird

How do you know when you have a good instrument? One, it will require prior knowledge. I’d encourage you to write down that prior knowledge into a DAG and use it to reflect on the feasibility of your design. As a starting point, you can contemplate identifying a causal effect using IV only if you can theoretically and logically defend the exclusion restriction, since the exclusion restriction is an untestable assumption. That defense requires theory, and since some people aren’t comfortable with theoretical arguments like that, they tend to eschew the use of IV. More and more applied microeconomists are skeptical of IV because they are able to tell limitless stories in which exclusion restrictions do not hold.

But, let’s say you think you do have a good instrument. How might you defend it as such to someone else? A necessary but not sufficient condition for having an instrument that can satisfy the exclusion restriction is if people are confused when you tell them about the instrument’s relationship to the outcome. Let me explain. No one is likely to be confused when you tell them that you think family size will reduce the labor supply of women. They don’t need a Becker model to convince them that women who have more children probably are employed outside the home less often than those with fewer children.

But what would they think if you told them that mothers whose first two children were the same gender were employed outside the home less than those whose two children had a balanced sex ratio? They would probably be confused because, after all, what does the gender composition of one’s first two children have to do with whether a woman works outside the home? That’s a head scratcher. They’re confused because, logically, whether the first two kids are the same gender versus not the same gender doesn’t seem on its face to change the incentives a women has to work outside the home, which is based on reservation wages and market wages. And yet, empirically it is true that if your first two children are a boy, many families will have a third compared to those who had a boy and a girl first. So what gives?

The gender composition of the first two children matters for a family if they have preferences over diversity of gender. Families where the first two children were boys are more likely to try again in the hopes they’ll have a girl. And the same for two girls. Insofar as parents would like to have at least one boy and one girl, then having two boys might cause them to roll the dice for a girl.

And there you see the characteristics of a good instrument. It’s weird to a lay person because a good instrument (two boys) only changes the outcome by first changing some endogenous treatment variable (family size) thus allowing us to identify the causal effect of family size on some outcome (labor supply). And so without knowledge of the endogenous variable, relationships between the instrument and the outcome don’t make much sense. Why? Because the instrument is irrelevant to the determinants of the outcome except for its effect on the endogenous treatment variable. You also see another quality of the instrument that we like, which is that it’s quasi-random.

Before moving along, I’d like to illustrate this “weird instrument” in one more way, using two of my favorite artists: Chance the Rapper and Kanye West. At the start of this chapter, I posted a line from Kanye West’s wonderful song “Ultralight Beam” on the underrated Life of Pablo. On that song, Chance the Rapper sings:

I made “Sunday Candy,” I’m never going to hell.
I met Kanye West, I’m never going to fail.

Several years before “Ultralight Beam,” Chance made a song called “Sunday Candy.” It’s a great song and I encourage you to listen to it. But Chance makes a strange argument here on “Ultralight Beam.” He claims that because he made “Sunday Candy,” therefore he won’t go to hell. Now even a religious person will find that perplexing, as there is nothing in Christian theology of eternal damnation that would link making a song to the afterlife. This, I would argue, is a “weird instrument” because without knowing the endogenous variable on the mediated path \(SC \rightarrow ? \rightarrow H\), the two phenomena don’t seem to go together.

But let’s say that I told you that after Chance made “Sunday Candy,” he got a phone call from his old preacher. The preacher loved the song and invited Chance to come sing it at church. And while revisiting his childhood church, Chance had a religious experience that caused him to convert back to Christianity. Now, and only now, does his statement make sense. It isn’t that “Sunday Candy” itself shaped the path of his afterlife, so much as “Sunday Candy” caused a particular event that itself caused his beliefs about the future to change. That the line makes a weird argument is what makes “Sunday Candy” a good instrument.

But let’s take the second line—“I met Kanye West, I’m never going to fail.” Unlike the first line, this is likely not a good instrument. Why? Because I don’t even need to know what variable is along the mediated path \(KW \rightarrow ? \rightarrow F\) to doubt the exclusion restriction. If you are a musician, a relationship with Kanye West can possibly make or break your career. Kanye could make your career by collaborating with you on a song or by introducing you to highly talented producers. There is no shortage of ways in which a relationship with Kanye West can cause you to be successful, regardless of whatever unknown endogenous variable we have placed in this mediated path. And since it’s easy to tell a story where knowing Kanye West directly causes one’s success, knowing Kanye West is likely a bad instrument. It simply won’t satisfy the exclusion restriction in this context.

Ultimately, good instruments are jarring precisely because of the exclusion restriction—these two things (gender composition and work) don’t seem to go together. If they did go together, it would likely mean that the exclusion restriction was violated. But if they don’t, then the person is confused, and that is at minimum a possible candidate for a good instrument. This is the commonsense explanation of the “only through” assumption.

7.3 Homogeneous Treatment Effects

There are two ways to discuss the instrumental variables design: one in a world where the treatment has the same causal effect for everybody (“homogeneous treatment effects”) and one in a world where the treatment effects can differ across the population (“heterogeneous treatment effects”). For homogeneous treatment effects, I will depend on a more traditional approach rather than on potential outcomes notation. When the treatment effect is constant, I don’t feel we need potential outcomes notation as much.

Instrumental variables methods are typically used to address omitted variable bias, measurement error, and simultaneity. For instance, quantity and price is determined by the intersection of supply and demand, so any observational correlation between price and quantity is uninformative about the elasticities associated with supply or demand curves. Philip Wright understood this, which was why he investigated the problem so intensely.

I will assume a homogeneous treatment effect of \(\delta\) which is the same for every person. This means that if college caused my wages to increase by 10%, it also caused your wages to increase by 10%. Let’s start by illustrating the problem of omitted variable bias. Assume the classical labor problem where we’re interested in the causal effect of schooling on earnings, but schooling is endogenous because of unobserved ability. Let’s draw a simple DAG to illustrate this setup.

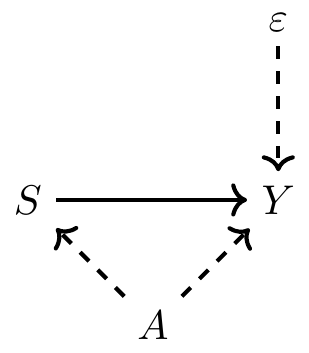
We can represent this DAG with a simple regression. Let the true model of earnings be:

\[ \begin{align} Y_i = \alpha + \delta S_i + \gamma A_i + \varepsilon_i \end{align} \]

where \(Y\) is the log of earnings, \(S\) is schooling measured in years, \(A\) is individual “ability,” and \(\varepsilon\) is an error term uncorrelated with schooling or ability. The reason \(A\) is unobserved is simply because the surveyor either forgot to collect it or couldn’t collect it and therefore it’s missing from the data set.³ For instance, the CPS tells us nothing about respondents’ family background, intelligence, motivation, or non-cognitive ability. Therefore, since ability is unobserved, we have the following equation instead:

\[ \begin{align} Y_i = \alpha + \delta S_i + \eta_i \end{align} \]

where \(\eta_i\) is a composite error term equalling \(\gamma A_i + \varepsilon_i\). We assume that schooling is correlated with ability, so therefore it is correlated with \(\eta_i\), making it endogenous in the second, shorter regression. Only \(\varepsilon_i\) is uncorrelated with the regressors, and that is by definition.

We know from the derivation of the least squares operator that the estimated value of \(\widehat{\delta}\) is:

\[ \begin{align} \widehat{\delta} = \dfrac{C(Y,S)}{V(S)} = \dfrac{E[YS] - E[Y]E[S]}{V(S)} \end{align} \]

Plugging in the true value of \(Y\) (from the longer model), we get the following:

\[ \begin{align} \widehat{\delta} & = \dfrac{E\big[\alpha S + S^2 \delta + \gamma SA + \varepsilon S\big] - E(S)E\big[\alpha + \delta S + \gamma A + \varepsilon\big]}{V(S)} \\ & = \dfrac{ \delta E(S^2) - \delta E(S)^2 + \gamma E(AS) - \gamma E(S)E(A) + E(\varepsilon S) - E(S)E(\varepsilon)}{V(S)} \\ & = \delta + \gamma \dfrac{C(AS)}{V(S)} \end{align} \]

If \(\gamma>0\) and \(C(A,S)>0\), then \(\widehat{\delta}\), the coefficient on schooling, is upward biased. And that is probably the case given that it’s likely that ability and schooling are positively correlated.

But let’s assume that you have found a really great weird instrument \(Z_i\) that causes people to get more schooling but that is independent of student ability and the structural error term. It is independent of ability, which means we can get around the endogeneity problem. And it’s not associated with the other unobserved determinants of earnings, which basically makes it weird. The DAG associated with this set up would look like this:

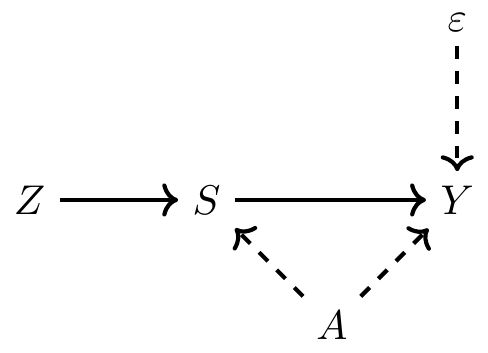
We can use this variable, as I’ll now show, to estimate \(\delta\). First, calculate the covariance of \(Y\) and \(Z\):

\[ \begin{align} C(Y,Z) & = C(\alpha + \delta S+\gamma A+\varepsilon, Z) \\ & = E\big[(\alpha+\delta S+\gamma A+\varepsilon),Z] - E(S) E(Z) \\ & =\big\{\alpha E(Z)- \alpha E(Z)\big\} + \delta \big\{E(SZ) - E(S)E(Z)\big\} \\ & \quad + \gamma \big\{E(AZ) - E(A)E(Z)\big\} + \big\{E(\varepsilon Z) - E(\varepsilon)E(Z)\big\} \\ & =\delta C(S,Z) + \gamma C(A,Z) + C(\varepsilon, Z) \end{align} \]

Notice that the parameter of interest, \(\delta\) is on the right side. So how do we isolate it? We can estimate it with the following:

\[ \begin{align} \widehat{\delta} = \dfrac{C(Y,Z)}{C(S,Z)} \end{align} \]

so long as \(C(A,Z)=0\) and \(C(\varepsilon,Z)=0\).

These zero covariances are the statistical truth contained in the IV DAG from earlier. If ability is independent of \(Z\), then this second covariance is zero. And if \(Z\) is independent of the structural error term, \(\varepsilon\), then it too is zero. This, you see, is what is meant by the “exclusion restriction”: the instrument must be independent of both parts of the composite error term.

But the exclusion restriction is only a necessary condition for IV to work; it is not a sufficient condition. After all, if all we needed was exclusion, then we could use a random number generator for an instrument. Exclusion is not enough. We also need the instrument to be highly correlated with the endogenous variable schooling \(S\). And the higher the better. We see that here because we are dividing by \(C(S,Z)\), so it necessarily requires that this covariance not be zero.

The numerator in this simple ratio is sometimes called the “reduced form,” while the denominator is called the “first stage.” These terms are somewhat confusing, particularly the former, as “reduced form” means different things to different people. But in the IV terminology, it is that relationship between the instrument and the outcome itself. The first stage is less confusing, as it gets its name from the two-stage least squares estimator, which we’ll discuss next.

When you take the probability limit of this expression, then assuming \(C(A,Z)=0\) and \(C(\varepsilon , Z)=0\) due to the exclusion restriction, you get \[ p\lim\ \widehat{\delta} = \delta \] But if \(Z\) is not independent of \(\eta\) (either because it’s correlated with \(A\) or \(\varepsilon\)), and if the correlation between \(S\) and \(Z\) is weak, then \(\widehat{\delta}\) becomes severely biased in finite samples.

7.3.1 Two-stage least squares

One of the more intuitive instrumental variables estimators is the two-stage least squares (2SLS). Let’s review an example to illustrate why it is helpful for explaining some of the IV intuition. Suppose you have a sample of data on \(Y\), \(S\), and \(Z\). For each observation \(i\), we assume the data are generated according to:

\[ \begin{align} Y_i & = \alpha + \delta S_i + \varepsilon_i \\ S_i & = \gamma + \beta Z_i + \epsilon_i \end{align} \]

where \(C(Z,\varepsilon)=0\) and \(\beta \neq 0\). The former assumption is the exclusion restriction whereas the second assumption is a non-zero first-stage. Now using our IV expression, and using the result that \(\sum_{i=1}^n(x_i -\bar{x})=0\), we can write out the IV estimator as:

\[ \begin{align} \widehat{\delta} & = \dfrac{C(Y,Z)}{C(S,Z)} \\ & = \dfrac{ \dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z})(Y_i - \overline{Y}) }{ \dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z}) (S_i - \overline{S})} \\ & =\dfrac{ \dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z})Y_i}{ \dfrac{1}{n} \sum_{i=1}^n (Z_i -\overline{Z})S_i} \end{align} \]

When we substitute the true model for \(Y\), we get the following:

\[ \begin{align} \widehat{\delta} & =\dfrac{ \dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z})\{\alpha + \delta S + \varepsilon \}}{\dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z})S_i} \\ & =\delta + \dfrac{ \dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z})\varepsilon_i}{ \dfrac{1}{n} \sum_{i=1}^n (Z_i - \overline{Z})S_i } \\ & =\delta + \text{``small if $n$ is large''} \end{align} \]

So, let’s return to our first description of \(\widehat{\delta}\) as the ratio of two covariances. With some simple algebraic manipulation, we get the following:

\[ \begin{align} \widehat{\delta} & =\dfrac{ C(Y,Z)}{C(S,Z)} \\ & =\dfrac{ \dfrac{C(Z,Y)}{V(Z)} }{\dfrac{ C(Z,S)}{V(Z)}} \end{align} \]

where the denominator is equal to \(\widehat{\beta}\).⁴ We can rewrite \(\widehat{\beta}\) as:

\[ \begin{align} \widehat{\beta} & = \dfrac{ C(Z,S)}{V(Z)} \\ \widehat{\beta}V(Z) & =C(Z,S) \end{align} \]

Then we rewrite the IV estimator and make a substitution:

\[ \begin{align} \widehat{\delta}_{IV} & =\dfrac{ C(Z,Y)}{C(Z,S)} \\ & =\dfrac{\widehat{\beta}C(Z,Y)}{\widehat{\beta} C(Z,S)} \\ & =\dfrac{ \widehat{\beta} C(Z,Y)}{\widehat{\beta}^2 V(Z)} \\ & = \dfrac{C(\widehat{\beta}Z,Y)}{V(\widehat{\beta}Z)} \end{align} \]

Notice now what is inside the parentheses: \(\widehat{\beta}Z\), which are the fitted values of schooling from the first-stage regression. We are no longer, in other words, using \(S\)—we are using its fitted values. Recall that \(S=\gamma + \beta Z + \epsilon\); \(\widehat{\delta} = \dfrac{ C(\widehat{\beta}ZY)}{V(\widehat{\beta}Z)}\) and let \(\widehat{S} = \widehat{\gamma} + \widehat{\beta}Z\). Then the two-stage least squares (2SLS) estimator is:

\[ \begin{align} \widehat{\delta}_{IV} & = \dfrac{ C(\widehat{\beta}Z,Y)}{V(\widehat{\beta}Z)} \\ & =\dfrac{C(\widehat{S},Y)}{V(\widehat{S})} \end{align} \]

I will now show that \(\widehat{\beta}C(Y,Z)=C(\widehat{S},Y)\), and leave it to you to show that \(V(\widehat{\beta}Z)=V(\widehat{S})\).

\[ \begin{align} C(\widehat{S},Y) & = E[\widehat{S}Y] - E[\widehat{S}]E[Y] \\ & = E\Big(Y[\widehat{\gamma}+\widehat{\beta}Z]\Big) - E(Y)E(\widehat{\gamma} + \widehat{\beta}Z) \\ & =\widehat{\gamma}E(Y) + \widehat{\beta}E(YZ) - \widehat{\gamma}E(Y) - \widehat{\beta}E(Y)E(Z) \\ & =\widehat{\beta}\big[E(YZ)-E(Y)E(Z)\big] \\ C(\widehat{S},Y) & = \widehat{\beta}C(Y,Z) \end{align} \]

Now let’s return to something I said earlier—learning 2SLS can help you better understand the intuition of instrumental variables more generally. What does this mean exactly? First, the 2SLS estimator used only the fitted values of the endogenous regressors for estimation. These fitted values were based on all variables used in the model, including the excludable instrument. And as all of these instruments are exogenous in the structural model, what this means is that the fitted values themselves have become exogenous too. Put differently, we are using only the variation in schooling that is exogenous. So that’s kind of interesting, as now we’re back in a world where we are identifying causal effects from exogenous changes in schooling caused by our instrument.

But, now the less-exciting news. This exogenous variation in \(S\) driven by the instrument is only a subset of the total variation in schooling. Or put differently, IV reduces the variation in the data, so there is less information available for identification, and what little variation we have left comes from only those units who responded to the instrument in the first place. This, it turns out, will be critical later when we relax the homogeneous treatment effects assumption and allow for heterogeneity.

7.4 Parental Methamphetamine Abuse and Foster Care

It’s helpful to occasionally stop and try to think about real-world applications as much as possible; otherwise the estimators feel very opaque and unhelpful. So to illustrate, I’m going to review one of my own papers with Keith Finlay that sought to estimate the effect that parental methamphetamine abuse had on child abuse and foster care admissions (Cunningham and Finlay 2012).

It has been claimed that substance abuse, notably illicit drug use, has a negative impact on parenting, causing neglect, but as these all occur in equilibrium, it’s possible that the correlation is simply reflective of selection bias. Maybe households with parents who abuse drugs would’ve had the same negative outcomes had the parents not used drugs. After all, it’s not like people are flipping coins when deciding to smoke meth. So let me briefly give you some background to the study so that you better understand the data-generating process.

First, methamphetamine is a toxic poison to the mind and body and highly addictive. Some of the symptoms of meth abuse are increased energy and alertness, decreased appetite, intense euphoria, impaired judgment, and psychosis. Second, the meth epidemic in the United States began on the West Coast, before gradually making its way eastward over the 1990s.

We were interested in the impact that this growth in meth abuse was having on children. Observers and law enforcement had commented, without concrete causal evidence, that the epidemic was causing a growth in foster care admissions. But how could we separate correlation from causality? The solution was contained within how meth itself is produced.

Meth is synthesized from a reduction of ephedrine or pseudoephedrine, which is also the active ingredient in many cold medications, such as Sudafed. Without one of these two precursors, it is impossible to produce the kind of meth people abuse. These precursors had supply chains that could be potentially disrupted because of the concentration of pharmaceutical laboratories. In 2004, nine factories manufactured the bulk of the world’s supply of ephedrine and pseudoephedrine. The US Drug Enforcement Agency correctly noted that if it could regulate access to ephedrine and pseudoephedrine, then it could effectively interrupt the production of methamphetamine, and in turn, hypothetically reduce meth abuse and its associated social harms.

So, with input from the DEA, Congress passed the Domestic Chemical Diversion Control Act in August 1995, which provided safeguards by regulating the distribution of products that contained ephedrine as the primary medicinal ingredient. But the new legislation’s regulations applied to ephedrine, not pseudoephedrine, and since the two precursors were nearly identical, traffickers quickly substituted. By 1996, pseudoephedrine was found to be the primary precursor in almost half of meth lab seizures.

Therefore, the DEA went back to Congress, seeking greater control over pseudoephedrine products. And the Comprehensive Methamphetamine Control Act of 1996 went into effect between October and December 1997. This act required distributors of all forms of pseudoephedrine to be subject to chemical registration. Dobkin and Nicosia (2009) argued that these precursor shocks may very well have been the largest supply shocks in the history of drug enforcement.

We placed a Freedom of Information Act request with the DEA requesting all of their undercover purchases and seizures of illicit drugs going back decades. The data included the price of an undercover purchase, the drug’s type, its weight and its purity, as well as the locations in which the purchases occurred. We used these data to construct a price series for meth, heroin, and cocaine. The effect of the two interventions were dramatic. The first supply intervention caused retail (street) prices (adjusted for purity, weight, and inflation) to more than quadruple. The second intervention, while still quite effective at raising relative prices, did not have as large an effect as the first. See Figure 7.1.

Figure 7.1: Ratio of Median Monthly Expected Retail Prices of Meth, Heroin, and Cocaine Relative to Their Respective Values in 1995, STRIDE 1995–1999. Reprinted from Cunningham and Finlay (2012).

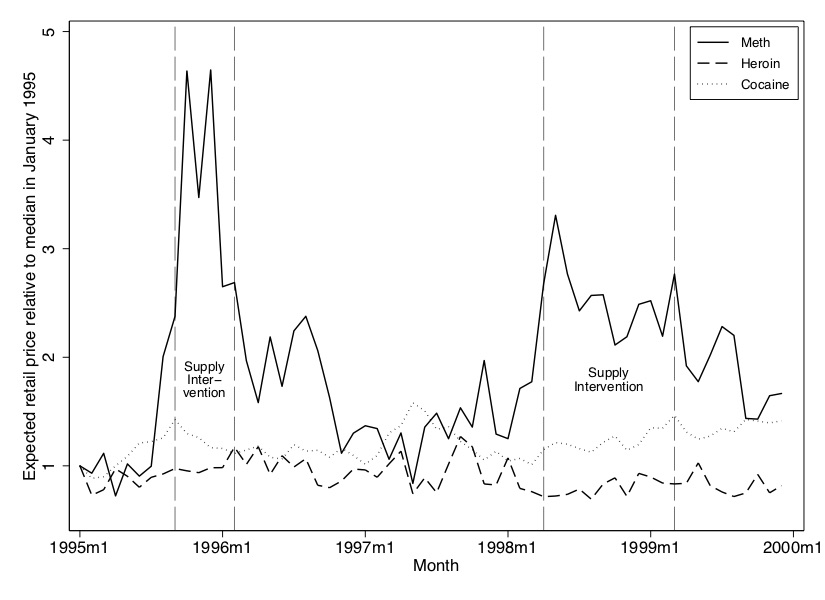
We showed two other drug prices (cocaine and heroin) in addition to meth because we wanted the reader to understand that the 1995 and 1997 shocks were uniquely impacting meth markets. They did not appear to be common shocks affecting all drug markets, in other words. As a result, we felt more confident that our analysis would be able to isolate the effect of methamphetamine, as opposed to substance abuse more generally. The two interventions simply had no effect on cocaine and heroin prices despite causing a massive shortage of meth and raising its retail price. It wouldn’t have surprised me if disrupting meth markets had caused a shift in demand for cocaine or heroin and in turn caused its prices to change, yet at first glance in the time series, I’m not finding that. Weird.

We are interested in the causal effect of meth abuse on child abuse, and so our first stage is necessarily a proxy for meth abuse—the number of people entering treatment who listed meth as one of the substances they used in their last episode of substance abuse. As I said before, since a picture is worth a thousand words, I’m going to show you pictures of both the first stage and the reduced form. Why do I do this instead of going directly to the tables of coefficients? Because quite frankly, you are more likely to find those estimates believable if you can see evidence for the first stage and the reduced form in the raw data itself.⁵

Figure 7.2: Visual representation of the equivalent of the first stage. Reprinted from Cunningham and Finlay (2012).

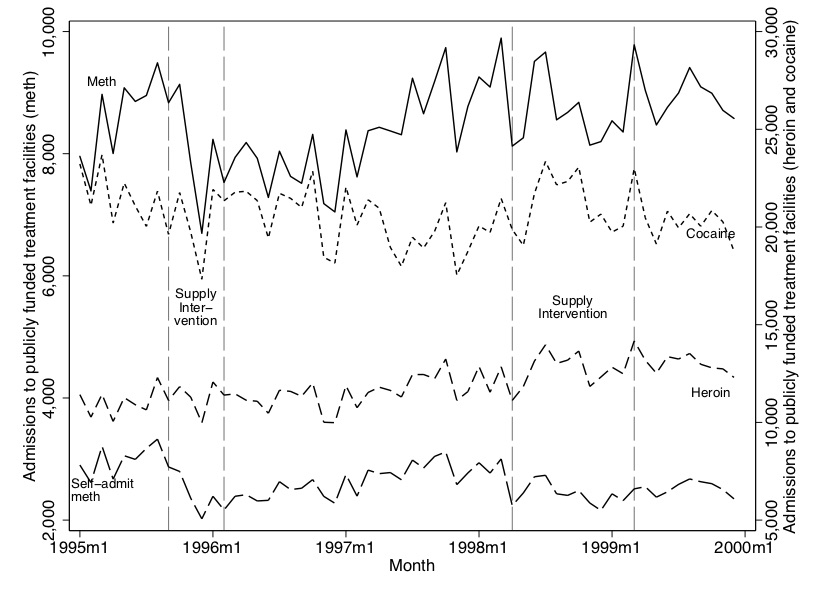
In Figure 7.2, we show the first stage. All of these data come from the Treatment Episode Data Set (TEDS), which includes all people going into treatment for substance abuse at federally funded clinics. Patients list the last three substances used in the most recent “episode.” We mark anyone who listed meth, cocaine, or heroin and aggregate by month and state. But first, let’s look at the national aggregate in Figure 7.2. You can see evidence for the effect the two interventions had on meth flows, particularly the ephedrine intervention. Self-admitted meth admissions dropped significantly, as did total meth admissions, but there’s no effect on cocaine or heroin. The effect of the pseudoephedrine is not as dramatic, but it appears to cause a break in trend as the growth in meth admissions slows during this period of time. In summary, it appears we have a first stage because, during the interventions, meth admissions declines.

In Figure 7.3, we show the reduced form—that is, the effect of the price shocks on foster care admissions. Consistent with what we found in our first-stage graphic, the ephedrine intervention in particular had a profoundly negative effect on foster care admissions. They fell from around 8,000 children removed per month to around 6,000, then began rising again. The second intervention also had an effect, though it appears to be milder. The reason we believe that the second intervention had a more modest effect than the first is because (1) the effect on price was about half the size of the first intervention, and (2) domestic meth production was being replaced by Mexican imports of meth over the late 1990s, and the precursor regulations were not applicable in Mexico. Thus, by the end of the 1990s, domestic meth production played a smaller role in total output, and hence the effect on price and admissions was probably smaller.

Figure 7.3: Figure 4 from Cunningham and Finlay (2012) showing reduced form effect of interventions on children removed from families and placed into foster care. Cunningham and Finlay (2012)

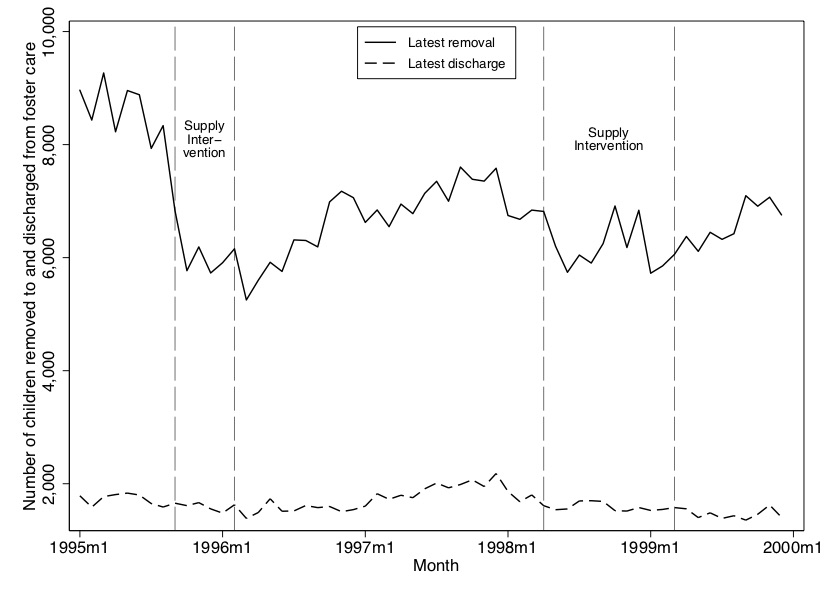
It’s worth reflecting for a moment on the reduced form. Why would rising retail prices of a pure gram of methamphetamine cause a child not to be placed in foster care? Prices don’t cause child abuse—they’re just nominal pieces of information in the world. The only way in which a higher price for meth could reduce foster care admissions is if parents reduced their consumption of methamphetamine, which in turn caused a reduction in harm to one’s child. This picture is a key piece of evidence for the reader that this is going on.

In Table 7.1, I reproduce our main results from my article with Keith. There are a few pieces of key information that all IV tables should have. First, there is the OLS regression. As the OLS regression suffers from endogeneity, we want the reader to see it so that they have something to compare the IV model to. Let’s focus on column 1, where the dependent variable is total entry into foster care. We find no effect, interestingly, of meth on foster care when we estimate using OLS.

Table 7.1: Log Latest Entry into Foster Care

	Log Latest Entry into Foster Care		Log Latest Entry into Child Neglect		Log Latest Entry into Physical Abuse
Covariates	OLS	2SLS	OLS	2SLS	OLS	2SLS
Log self-referred	0.001	1.54\(^{***}\)	0.03	1.03\(^{***}\)	0.04	1.49\(^{**}\)
Meth treatment rate	(0.02)	(0.59)	(0.02)	(0.41)	(0.03)	(0.62)
Month-of-year fixed effects	Yes	Yes	Yes	Yes	Yes	Yes
State controls	Yes	Yes	Yes	Yes	Yes	Yes
State fixed effects	Yes	Yes	Yes	Yes	Yes	Yes
State linear time trends	Yes	Yes	Yes	Yes	Yes	Yes
First Stage Instrument
Price deviation instrument		\(-0.0005^{***}\)		\(-0.0005^{***}\)		\(-0.0005^{**}\)
		(0.0001)		(0.0001)		(0.0001)
\(F\)-statistic for IV in first stage		17.60		17.60		17.60
\(N\)	1,343	1,343		1,343		1,343

Notes: Log latest entry into foster care is the natural log of the sum of all new foster care admissions by state, race, and month. Models 3 to 10 denote the flow of children into foster care via a given route of admission denoted by the column heading. Models 11 and 12 use the natural log of the sum of all foster care exits by state, race and month. \(^{***}\), \(^{**}\), and \(^{*}\) denote statistical significance at the 1%, 5%, and 10% levels, respectively.

The second piece of information that one should report in a 2SLS table is the first stage itself. We report the first stage at the bottom of each even-numbered column. As you can see, for each one-unit deviation in price from its long-term trend, meth admissions into treatment (our proxy) fell by \(-0.0005\) log points. This is highly significant at the 1% level, but we check for the strength of the instrument using the \(F\) statistic (Staiger and Stock 1997).⁶ We have an \(F\) statistic of 17.6, which suggests that our instrument is strong enough for identification.

Finally, let’s examine the 2SLS estimate of the treatment effect itself. Notice using only the exogenous variation in log meth admissions, and assuming the exclusion restriction holds in our model, we are able to isolate a causal effect of log meth admissions on log aggregate foster care admissions. As this is a log-log regression, we can interpret the coefficient as an elasticity. We find that a 10% increase in meth admissions for treatment appears to cause around a 15% increase in children being removed from their homes and placed into foster care. This effect is both large and precise. And it was not detectable otherwise (the coefficient was zero).

Why are they being removed? Our data (AFCARS) lists several channels: parental incarceration, child neglect, parental drug use, and physical abuse. Interestingly, we do not find any effect of parental drug use or parental incarceration, which is perhaps counterintuitive. Their signs are negative and their standard errors are large. Rather, we find effects of meth admissions on removals for physical abuse and neglect. Both are elastic (i.e., \(\delta >1\)).

What did we learn? First, we learned how a contemporary piece of applied microeconomics goes about using instrumental variables to identify causal effects. We saw the kinds of graphical evidence mustered, the way in which knowledge about the natural experiment and the policies involved helped the authors argue for the exclusion restriction (since it cannot be tested), and the kind of evidence presented from 2SLS, including the first-stage tests for weak instruments. Hopefully seeing a paper at this point was helpful. But the second thing we learned concerned the actual study itself. We learned that for the group of meth users whose behavior was changed as a result of rising real prices of a pure gram of methamphetamine (i.e., the complier subpopulation), their meth use was causing child abuse and neglect so severe that it merited removing their children and placing those children into foster care. If you were only familiar with Dobkin and Nicosia (2009), who found no effect of meth on crime using county-level data from California and only the 1997 ephedrine shock, you might incorrectly conclude that there are no social costs associated with meth abuse. But, while meth does not appear to cause crime in California, it does appear to harm the children of meth users and places strains on the foster care system.

7.5 The Problem of Weak Instruments

I am not trying to smother you with papers. But before we move back into the technical material itself, I’d like to discuss one more paper. This paper will also help you better understand the weak instrument literature following its publication.

As we’ve said since the beginning, with example after example, there is a very long tradition in labor economics of building models that can credibly identify the returns to schooling. This goes back to Becker (1994) and the workshop at Columbia that Becker ran for years with Jacob Mincer. This study of the returns to schooling has been an important task given education’s growing importance in the distribution of income and wealth since the latter twentieth century with increasing returns to skill in the marketplace (Juhn, Murphy, and Pierce 1993).

One of the more seminal papers in instrumental variables for the modern period is Angrist and Krueger (1991). Their idea is simple and clever; a quirk in the United States educational system is that a child enters a grade on the basis of his or her birthday. For a long time, that cutoff was late December. If children were born on or before December 31, then they were assigned to the first grade. But if their birthday was on or after January 1, they were assigned to kindergarten. Thus two people—one born on December 31 and one born on January 1—were exogenously assigned different grades.

Now there’s nothing necessarily relevant here because if those children always stay in school for the duration necessary to get a high school degree, then that arbitrary assignment of start date won’t affect high school completion. It’ll only affect when they get that high school degree. But this is where it gets interesting. For most of the twentieth century, the US had compulsory schooling laws that forced a person to remain in high school until age 16. After age 16, one could legally stop going to school. Figure 7.4 explains visually this instrumental variable.⁷

Figure 7.4: Compulsory schooling start dates by birthdates.

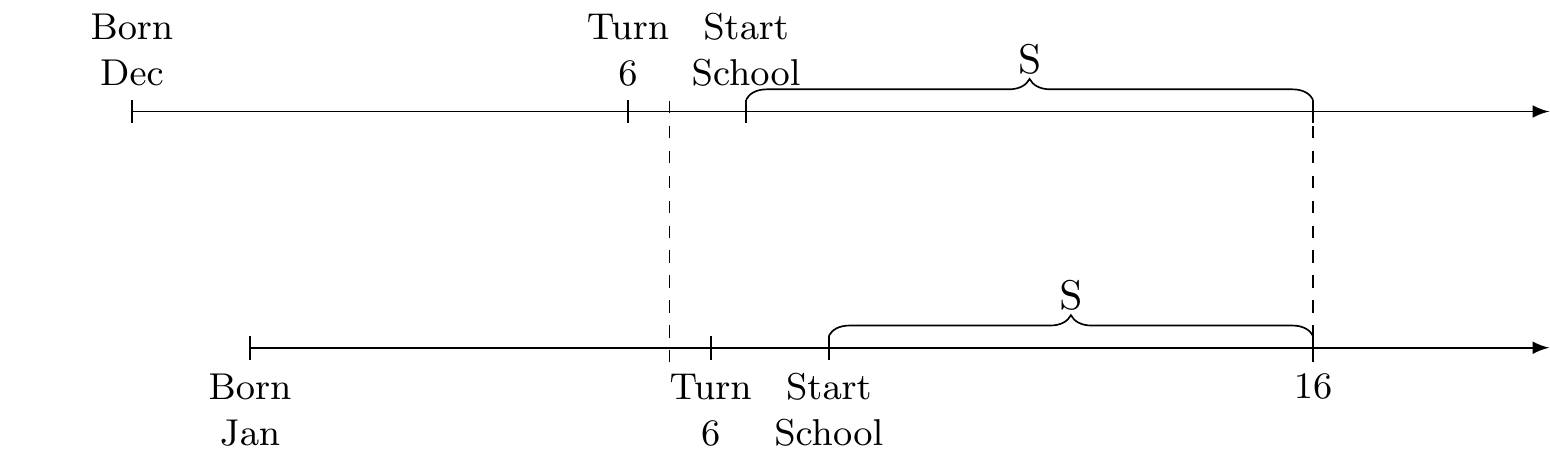
Angrist and Krueger had the insight that that small quirk was exogenously assigning more schooling to people born later in the year. The person born in December would reach age 16 with more education than the person born in January, in other words. Thus, the authors uncovered small exogenous variation in schooling. Notice how similar their idea was to regression discontinuity. That’s because IV and RDD are conceptually very similar strategies.

Figure 7.5: First stage relationship between quarter of birth and schooling. Reprinted from Angrist and Krueger (1991).

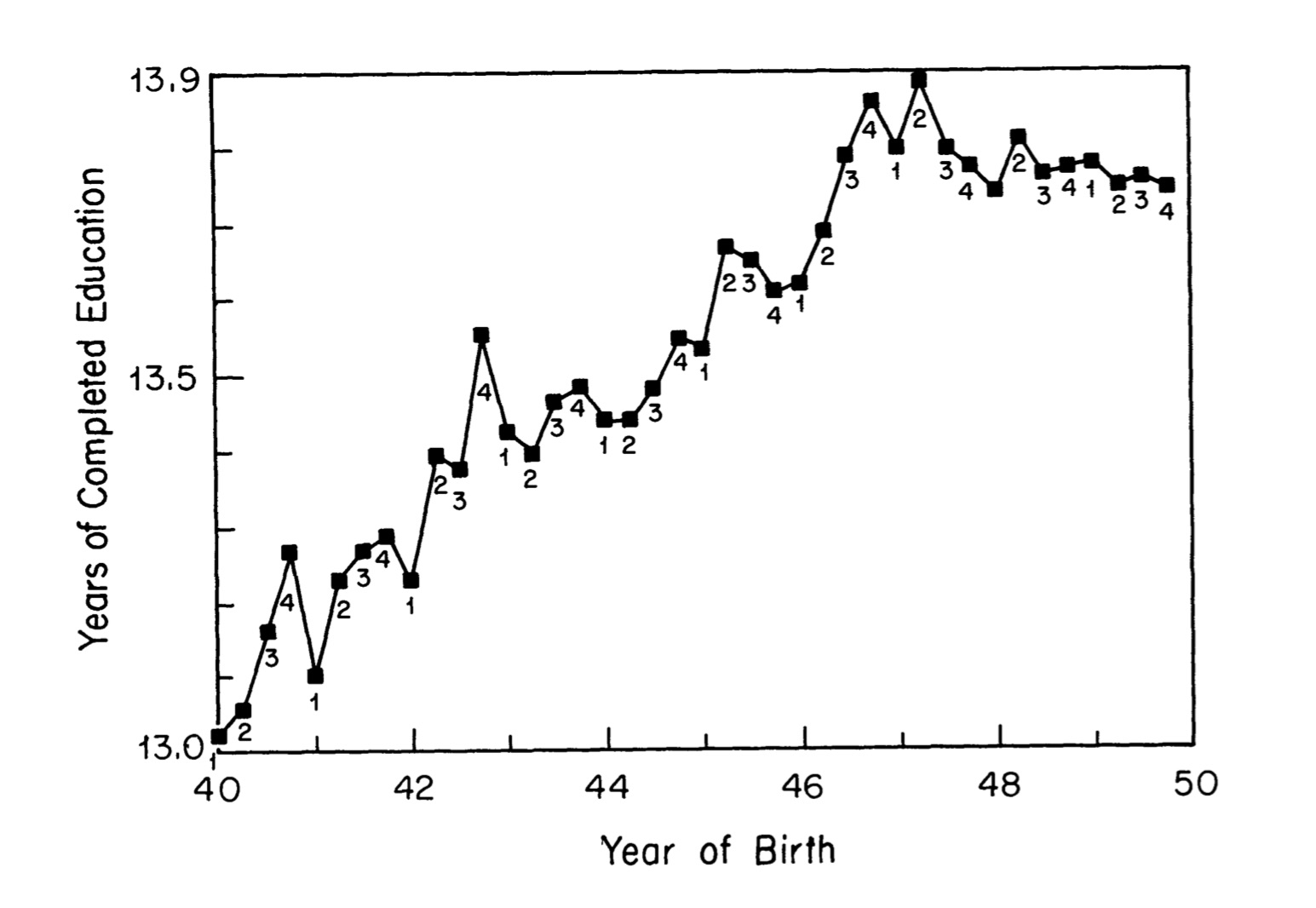
Figure 7.5 shows the first stage, and it is really interesting. Look at all those 3s and 4s at the top of the picture. There’s a clear pattern—those with birthdays in the third and fourth quarter have more schooling on average than do those with birthdays in the first and second quarters. That relationship gets weaker as we move into later cohorts, but that is probably because for later cohorts, the price on higher levels of schooling was rising so much that fewer and fewer people were dropping out before finishing their high school degree.

Figure 7.6: Reduced form visualization of the relationship between quarter of birth and log weekly earnings. Reprinted from Angrist and Krueger (1991).

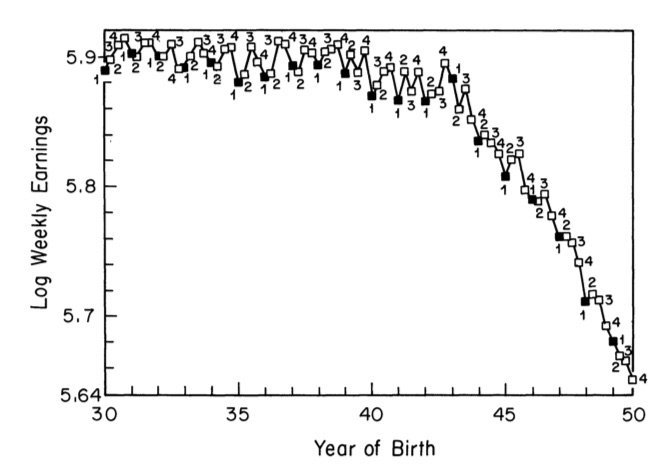
Figure 7.6 shows the reduced-form relationship between quarter of birth and log weekly earnings.⁸ You have to squint a little bit, but you can see the pattern—all along the top of the jagged path are 3s and 4s, and all along the bottom of the jagged path are 1s and 2s. Not always, but it’s correlated.

Remember what I said about how instruments having a certain ridiculousness to them? That is, you know you have a good instrument if the instrument itself doesn’t seem relevant for explaining the outcome of interest because that’s what the exclusion restriction implies. Why would quarter of birth affect earnings? It doesn’t make any obvious, logical sense why it should. But, if I told you that people born later in the year got more schooling than those with less because of compulsory schooling, then the relationship between the instrument and the outcome snaps into place. The only reason we can think of as to why the instrument would affect earnings is if the instrument were operating through schooling. Instruments only explain the outcome, in other words, when you understand their effect on the endogenous variable.⁹

Angrist and Krueger use three dummies as their instruments: a dummy for first quarter, a dummy for second quarter, and a dummy for third quarter. Thus, the omitted category is the fourth quarter, which is the group that gets the most schooling. Now ask yourself this: if we regressed years of schooling onto those three dummies, what should the signs and magnitudes be? That is, what would we expect the relationship between the first quarter (compared to the fourth quarter) and schooling? Let’s look at their first-stage results (Table 7.2).

Table 7.2: Quarter of birth and schooling

		Quarter of Birth Effect
Outcome variable	Birth Cohort	I	II	III
Total schooling	1930-1939	-0.124	-0.86	-0.015
		(0.017)	(0.017)	(0.016)
	1940–1949	\(-0.085\)	\(-0.035\)	\(-0.017\)
		(0.012)	(0.012)	(0.011)
High school grad	1930-1939	\(-0.019\)	\(-0.020\)	\(-0.004\)
		(0.002)	(0.002)	(0.002)
	1940–1949	\(-0.015\)	\(-0.012\)	\(-0.002\)
		(0.001)	(0.001)	(0.001)
College grad	1930-1939	\(-0.005\)	0.003	0.002
		(0.002)	(0.002)	(0.002)
	1940–1949	\(-0.003\)	0.004	0.000
		(0.002)	(0.002)	(0.002)

Standard errors in parenthesis.

Table 7.2 shows the first stage from a regression of the following form: \[ S_i=X\pi_{10}+Z_1\pi_{11}+Z_2\pi_{12}+Z_3\pi_{13}+\eta_1 \] where \(Z_i\) is the dummy for the first three quarters, and \(\pi_i\) is the coefficient on each dummy. Now we look at what they produced in Table 7.2. The coefficients are all negative and significant for the total years of education and the high school graduate dependent variables. Notice, too, that the relationship gets much weaker once we move beyond the groups bound by compulsory schooling: the number of years of schooling for high school students (no effect) and probability of being a college graduate (no effect).

Regarding those college non-results. Ask yourself this question: why should we expect quarter of birth to affect the probability of being a high school graduate but not a college grad? What if we had found quarter of birth predicted high school completion, college completion, post-graduate completion, and total years of schooling beyond high school? Wouldn’t it start to seem like this compulsory schooling instrument was not what we thought it was? After all, this quarter of birth instrument really should only impact high school completion; since it doesn’t bind anyone beyond high school, it shouldn’t affect the number of years beyond high school or college completion probabilities. If it did, we might be skeptical of the whole design. But here it didn’t, which to me makes it even more convincing that they’re identifying a compulsory high school schooling effect.¹⁰

Now we look at the second stage for both OLS and 2SLS (which the authors label TSLS, but means the same thing). Table 7.3 shows these results. The authors didn’t report the first stage in this table because they reported it in the earlier table we just reviewed. For small values, the log approximates a percentage change, so they are finding a 7.1% return for every additional year of schooling, but with 2SLS it’s higher (8.9%). That’s interesting, because if it was merely ability bias, then we’d expect the OLS estimate to be too large, not too small. So something other than mere ability bias must be going on here.

Table 7.3: Effect of schooling on wages using OLS and 2SLS

Independent variable	OLS	2SLS
Years of schooling	0.0711	0.0891
	(0.0003)	(0.0161)
9 Year-of-birth rummies	Yes	Yes
8 Region-of-residence dummies	No	No

Standard errors in parenthesis. First stage is quarter of birth dummies.

For whatever it’s worth, I am personally convinced at this point that quarter of birth is a valid instrument and that they’ve identified a causal effect of schooling on earnings, but Angrist and Krueger (1991) want to go further, probably because they want more precision in their estimate. And to get more precision, they load up the first stage with even more instruments. Specifically, they use specifications with 30 dummies (quarter of birth \(\times\) year) and 150 dummies (quarter of birth \(\times\) state) as instruments. The idea is that the quarter of birth effect may differ by state and cohort.

But at what cost? Many of these instruments are only now weakly correlated with schooling—in some locations, they have almost no correlation, and for some cohorts as well. We got a flavor of that, in fact, in Table 7.3, where the later cohorts show less variation in schooling by quarter of birth than the earlier cohorts. What is the effect, then, of reducing the variance in the estimator by loading up the first stage with a bunch of noise?

Bound, Jaeger, and Baker (1995) is a classic work in what is sometimes called the “weak instrument” literature. It’s in this paper that we learn some some very basic problems created by weak instruments, such as the form of 2SLS bias in finite samples. Since Bound, Jaeger, and Baker (1995) focused on the compulsory schooling application that Angrist and Krueger (1991) had done, I will stick with that example throughout. Let’s consider their model with a single endogenous regressor and a simple constant treatment effect. The causal model of interest here is as before: \[ y=\beta s + \varepsilon \] where \(y\) is some outcome and \(s\) is some endogenous regressor, such as schooling. Our instrument is \(Z\) and the first-stage equation is: \[ s=Z' \pi + \eta \] Let’s start off by assuming that \(\varepsilon\) and \(\eta\) are correlated. Then estimating the first equation by OLS would lead to biased results, wherein the OLS bias is: \[ E\big[\widehat{\beta}_{OLS}-\beta\big] = \dfrac{C(\varepsilon, s)}{V(s)} \] We will rename this ratio as \(\dfrac{\sigma_{\varepsilon \eta}}{\sigma^2_s}\). Bound, Jaeger, and Baker (1995) show that the bias of 2SLS centers on the previously defined OLS bias as the weakness of the instrument grows. Following Angrist and Pischke (2009), I’ll express that bias as a function of the first-stage \(F\) statistic: \[ E\big[\widehat{\beta}_{2SLS}-\beta\big] \approx \dfrac{\sigma_{\varepsilon \eta}}{\sigma_\eta^2} \dfrac{1}{F+1} \] where \(F\) is the population analogy of the \(F\)-statistic for the joint significance of the instruments in the first-stage regression. If the first stage is weak, and \(F\rightarrow 0\), then the bias of 2SLS approaches \(\dfrac{\sigma_{\varepsilon \eta}}{\sigma_\eta^2}\). But if the first stage is very strong, \(F \rightarrow \infty\), then the 2SLS bias goes to 0.

Returning to our rhetorical question from earlier, what was the cost of adding instruments without predictive power? Adding more weak instruments causes the first-stage \(F\) statistic to approach zero and increase the bias of 2SLS.

Bound, Jaeger, and Baker (1995) studied this empirically, replicating Angrist and Krueger (1991), and using simulations. Table 7.4 shows what happens once they start adding in controls. Notice that as they do, the \(F\) statistic on the excludability of the instruments falls from 13.5 to 4.7 to 1.6. So by the \(F\) statistic, they are already running into a weak instrument once they include the 30 quarter of birth \(\times\) year dummies, and I think that’s because as we saw, the relationship between quarter of birth and schooling got smaller for the later cohorts.

Table 7.4: Effect of completed schooling on men’s log weekly wages

Independent variable	OLS	2SLS	OLS	2SLS	OLS	2SLS
Years of schooling	0.063	0.142	0.063	0.081	0.063	0.060
	(0.000)	(0.033)	(0.000)	(0.016)	(0.000)	(0.029)
First stage \(F\)		13.5		4.8		1.6
Excluded instruments
Quarter of birth		Yes		Yes		Yes
Quarter of birth \(\times\) year of birth		No		Yes		Yes
Number of excluded instruments		3		30		28

Standard errors in parenthesis. First stage is quarter of birth dummies.

Next, they added in the weak instruments—all 180 of them—which is shown in Table 7.5. And here we see that the problem persists. The instruments are weak, and therefore the bias of the 2SLS coefficient is close to that of the OLS bias.

Table 7.5: Effect of completed schooling on men’s log weekly wages controlling for state of birth

Independent variable	OLS	2SLS	OLS	2SLS
Years of schooling	0.063	0.083	0.063	0.081
	(0.000)	(0.009)	(0.000)	(0.011)
First stage \(F\)		2.4		1.9
Excluded instruments
Quarter of birth		Yes		Yes
Quarter of birth \(\times\) year of birth		Yes		Yes
Quarter of birth \(\times\) state of birth		Yes		Yes
Number of excluded instruments		180		178

Standard errors in parenthesis.

But the really damning part of the Bound, Jaeger, and Baker (1995) was their simulation. The authors write:

To illustrate that second-stage results do not give us any indication of the existence of quantitatively important finite-sample biases, we reestimated Table 1, columns (4) and (6) and Table 2, columns (2) and (4), using randomly generated information in place of the actual quarter of birth, following a suggestion by Alan Krueger. The means of the estimated standard errors reporting in the last row are quite close to the actual standard deviations of the 500 estimates for each model. . . . It is striking that the second-stage results reported in Table 3 look quite reasonable even with no information about educational attainment in the simulated instruments. They give no indication that the instruments were randomly generated\(\ldots\) On the other hand, the F statistics on the excluded instruments in the first-stage regressions are always near their expected value of essentially 1 and do give a clear indication that the estimates of the second-stage coefficients suffer from finite-sample biases. Bound, Jaeger, and Baker (1995) (p.448)

So, what can you do if you have weak instruments? Unfortunately, not a lot. You can use a just-identified model with your strongest IV. Second, you can use a limited-information maximum likelihood estimator (LIML). This is approximately median unbiased for over identified constant effects models. It provides the same asymptotic distribution as 2SLS under homogeneous treatment effects but provides a finite-sample bias reduction.

But, let’s be real for a second. If you have a weak instrument problem, then you only get so far by using LIML or estimating a just-identified model. The real solution for a weak instrument problem is to get better instruments. Under homogeneous treatment effects, you’re always identifying the same effect, so there’s no worry about a complier only parameter. So you should just continue searching for stronger instruments that simultaneously satisfy the exclusion restriction.¹¹

In conclusion, I think we’ve learned a lot about instrumental variables and why they are so powerful. The estimators based on this design are capable of identifying causal effects when your data suffer from selection on unobservables. Since selection on unobservables is believed to be very common, this is a very useful methodology for addressing that. But, that said, we also have learned some of the design’s weaknesses, and hence why some people eschew it. Let’s now move to heterogeneous treatment effects so that we can better understand some limitations a bit better.

7.6 Heterogeneous Treatment Effects

Now we turn to a scenario where we relax the assumption that treatment effects are the same for every unit. This is where the potential outcomes notation comes in handy. Instead, we will allow for each unit to have a unique response to the treatment, or \[ Y_i^1 - Y_i^0 = \delta_i \] Note that the treatment effect parameter now differs by individual \(i\). We call this heterogeneous treatment effects.

The main questions we have now are: (1) what is IV estimating when we have heterogeneous treatment effects, and (2) under what assumptions will IV identify a causal effect with heterogeneous treatment effects? The reason this matters is that once we introduce heterogeneous treatment effects, we introduce a distinction between the internal validity of a study and its external validity. Internal validity means our strategy identified a causal effect for the population we studied. But external validity means the study’s finding applied to different populations (not in the study). The deal is that under homogeneous treatment effects, there is no tension between external and internal validity because everyone has the same treatment effect. But under heterogeneous treatment effects, there is huge tension; the tension is so great, in fact, that it may even undermine the meaningfulness of the relevance of the estimated causal effect despite an otherwise valid IV design!¹²

Heterogeneous treatment effects are built on top of the potential outcomes notation, with a few modifications. Since now we have two arguments—\(D\) and \(Z\)—we have to modify the notation slightly. We say that \(Y\) is a function of \(D\) and \(Z\) as \(Y_i(D_i=0,Z_i=1)\), which is represented as \(Y_i(0,1)\).

Potential outcomes as we have been using the term refers to the \(Y\) variable, but now we have a new potential variable—potential treatment status (as opposed to observed treatment status). Here are the characteristics:

\[ \begin{align} D_i^1 & =i\text{'s treatment status when }Z_i=1 \\ D_i^0 & =i\text{'s treatment status when }Z_i=0 \end{align} \]

And observed treatment status is based on a treatment status switching equations:

\[ \begin{align} D_i &=&D_i^0 + (D_i^1 - D_i^0)Z_i \\ &=&\pi_0 + \pi_1 Z_i + \phi_i \end{align} \]

where \(\pi_{0i}=E[D_i^0]\), \(\pi_{1i} = (D_i^1 - D_i^0)\) is the heterogeneous causal effect of the IV on \(D_i\), and \(E[\pi_{1i}]=\) the average causal effect of \(Z_i\) on \(D_i\).

There are considerably more assumptions necessary for identification once we introduce heterogeneous treatment effects—specifically five assumptions. We now review each of them. And to be concrete, I use repeatedly as an example the effect of military service on earnings using a draft lottery as the instrumental variable (Angrist 1990). In that paper, Angrist estimated the returns to military service using as an instrument the person’s draft lottery number. The draft lottery number was generated by a random number generator and if a person’s number was in a particular range, they were drafted, otherwise they weren’t.

First, as before, there is a stable unit treatment value assumption (SUTVA) that states that the potential outcomes for each person \(i\) are unrelated to the treatment status of other individuals. The assumption states that if \(Z_i=Z_i'\), then \(D_i(Z) = D_i(Z')\). And if \(Z_i=Z_i'\) and \(D_i=D_i'\), then \(Y_i(D,Z)=Y_i(D',Z')\). A violation of SUTVA would be if the status of a person at risk of being drafted was affected by the draft status of others at risk of being drafted. Such spillovers violate SUTVA.¹³ Not knowing a lot about how that works, I can’t say whether Angrist’s draft study would’ve violated SUTVA. But it seems like he’s safe to me.

Second, there is the independence assumption. The independence assumption is also sometimes called the “as good as random assignment” assumption. It states that the IV is independent of the potential outcomes and potential treatment assignments. Notationally, it is \[ \Big\{Y_i(D_i^1,1), Y_i(D_i^0,0),D_i^1,D_i^0\Big\} \independent Z_i \] The independence assumption is sufficient for a causal interpretation of the reduced form:

\[ \begin{align} E\big[Y_i\mid Z_i=1\big]-E\big[Y_i\mid Z_i=0\big] & = E\big[Y_i(D_i^1,1)\mid Z_i=1\mid]- E\big[Y_i(D_i^0,0)\mid Z_i=0\big] \\ & = E[Y_i(D_i^1,1)] - E[Y_i(D_i^0,0)] \end{align} \]

And many people may actually prefer to work just with the instrument and its reduced form because they find independence satisfying and acceptable. The problem, though, is technically the instrument is not the program you’re interested in studying. And there may be many mechanisms leading from the instrument to the outcome that you need to think about (as we will see below). Ultimately, independence is nothing more and nothing less than assuming that the instrument itself is random.

Independence means that the first stage measures the causal effect of \(Z_i\) on \(D_i\):

\[ \begin{align} E\big[D_i\mid Z_i=1\big]-E\big[D_i\mid Z_i=0\big] & = E\big[D_i^1\mid Z_i=1\big] - E\big[D_i^0\mid Z_i=0\big] \\ & = E[D_i^1 - D_i^0] \end{align} \]

An example of this is if Vietnam conscription for military service was based on randomly generated draft lottery numbers. The assignment of draft lottery number was independent of potential earnings or potential military service because it was “as good as random.”

Third, there is the exclusion restriction. The exclusion restriction states that any effect of \(Z\) on \(Y\) must be via the effect of \(Z\) on \(D\). In other words, \(Y_i(D_i,Z_i)\) is a function of \(D_i\) only. Or formally: \[ Y_i(D_i,0) = Y_i(D_i,1)\quad \text{for $D=0,1$} \] Again, our Vietnam example. In the Vietnam draft lottery, an individual’s earnings potential as a veteran or a non-veteran are assumed to be the same regardless of draft eligibility status. The exclusion restriction would be violated if low lottery numbers affected schooling by people avoiding the draft. If this was the case, then the lottery number would be correlated with earnings for at least two cases. One, through the instrument’s effect on military service. And two, through the instrument’s effect on schooling. The implication of the exclusion restriction is that a random lottery number (independence) does not therefore imply that the exclusion restriction is satisfied. These are different assumptions.

Fourth is the first stage. IV designs require that \(Z\) be correlated with the endogenous variable such that \[ E[D_i^1 - D_i^0] \ne 0 \] \(Z\) has to have some statistically significant effect on the average probability of treatment. An example would be having a low lottery number. Does it increase the average probability of military service? If so, then it satisfies the first stage requirement. Note, unlike independence and exclusion, the first stage is testable as it is based solely on \(D\) and \(Z\), both of which you have data on.

And finally, there is the monotonicity assumption. This is only strange at first glance but is actually quite intuitive. Monotonicity requires that the instrumental variable (weakly) operate in the same direction on all individual units. In other words, while the instrument may have no effect on some people, all those who are affected are affected in the same direction (i.e., positively or negatively, but not both). We write it out like this: \[ \text{Either $\pi_{1i} \geq 0$ for all $i$ or $\pi_{1i} \leq 0$ for all $i=1,\dots, N$} \] What this means, using our military draft example, is that draft eligibility may have no effect on the probability of military service for some people, like patriots, people who love and want to serve their country in the military, but when it does have an effect, it shifts them all into service, or out of service, but not both. The reason we have to make this assumption is that without monotonicity, IV estimators are not guaranteed to estimate a weighted average of the underlying causal effects of the affected group.

If all five assumptions are satisfied, then we have a valid IV strategy. But that being said, while valid, it is not doing what it was doing when we had homogeneous treatment effects. What, then, is the IV strategy estimating under heterogeneous treatment effects? Answer: the local average treatment effect (LATE) of \(D\) on \(Y\):

\[ \begin{align} \delta_{IV,LATE} & =\dfrac{ \text{Effect of $Z$ on $Y$}}{\text{Effect of $Z$ on $D$}} \\ & =\dfrac{E\big[Y_i(D_i^1,1)-Y_i(D_i^0,0)\big]}{ E[D_i^1 - D_i^0]} \\ & =E\big[(Y_i^1-Y_i^0)\mid D_i^1-D_i^0=1\big] \end{align} \]

The LATE parameter is the average causal effect of \(D\) on \(Y\) for those whose treatment status was changed by the instrument, \(Z\). We know that because notice the difference in the last line: \(D_i^1 - D_i^0\). So, for those people for whom that is equal to 1, we calculate the difference in potential outcomes. Which means we are only averaging over treatment effects for whom \(D_i^1 - D_i^0\). Hence why the parameter we are estimating is “local.”

How do we interpret Angrist’s estimated causal effect in his Vietnam draft project? Well, IV estimates the average effect of military service on earnings for the subpopulations who enrolled in military service because of the draft. These are specifically only those people, though, who would not have served otherwise. It doesn’t identify the causal effect on patriots who always serve, for instance, because \(D_i^1 - D_i^0 = 0\) for patriots. They always serve! \(D_i^1=1\) and \(D_i^0=1\) for patriots because they’re patriots! It also won’t tell us the effect of military service on those who were exempted from military service for medical reasons because for these people \(D_i^1=0\) and \(D_i^0=0\).¹⁴

The LATE framework has even more jargon, so let’s review it now. The LATE framework partitions the population of units with an instrument into potentially four mutually exclusive groups. Those groups are:

1. Compliers: This is the subpopulation whose treatment status is affected by the instrument in the correct direction. That is, \(D_i^1=1\) and \(D_i^0=0\).

2. Defiers: This is the subpopulation whose treatment status is affected by the instrument in the wrong direction. That is, \(D_i^1=0\) and \(D_i^0=1\).¹⁵

3. Never takers: This is the subpopulation of units that never take the treatment regardless of the value of the instrument. So, \(D_i^1=D_i^0=0\). They simply never take the treatment.¹⁶

4. Always takers: This is the subpopulation of units that always take the treatment regardless of the value of the instrument. So, \(D_i^1=D_i^0=1\). They simply always take the instrument.¹⁷

As outlined above, with all five assumptions satisfied, IV estimates the average treatment effect for compliers, which is the parameter we’ve called the local average treatment effect. It’s local in the sense that it is average treatment effect to the compliers only. Contrast this with the traditional IV pedagogy with homogeneous treatment effects. In that situation, compliers have the same treatment effects as non-compliers, so the distinction is irrelevant. Without further assumptions, LATE is not informative about effects on never-takers or always-takers because the instrument does not affect their treatment status.

Does this matter? Yes, absolutely. It matters because in most applications, we would be mostly interested in estimating the average treatment effect on the whole population, but that’s not usually possible with IV.¹⁸

Now that we have reviewed the basic idea and mechanics of instrumental variables, including some of the more important tests associated with it, let’s get our hands dirty with some data. We’ll work with a couple of data sets now to help you better understand how to implement 2SLS in real data.

Causal Inference:
The Mixtape.

Buy the print version today:

Buy from Amazon Buy from Yale Press

7.7 Applications

7.7.1 College in the county

We will once again look at the returns to schooling since it is such a historically popular topic for causal questions in labor. In this application, we will simply estimate a 2SLS model, calculate the first-stage F statistic, and compare the 2SLS results with the OLS results. I will be keeping it simple, because my goal is just to help the reader become familiarized with the procedure.

The data comes from the NLS Young Men Cohort of the National Longitudinal Survey. This data began in 1966 with 5,525 men aged 14–24 and continued to follow up with them through 1981. These data come from 1966, the baseline survey, and there are a number of questions related to local labor-markets. One of them is whether the respondent lives in the same county as a 4-year (and a 2-year) college.

Card (1995) is interested in estimating the following regression equation: \[ Y_i=\alpha+\delta S_i + \gamma X_i+\varepsilon_i \] where \(Y\) is log earnings, \(S\) is years of schooling, \(X\) is a matrix of exogenous covariates, and \(\varepsilon\) is an error term that contains, among other things, unobserved ability. Under the assumption that \(\varepsilon\) contains ability, and ability is correlated with schooling, then \(C(S,\varepsilon)\neq 0\) and therefore schooling is biased. Card (1995) proposes therefore an instrumental variables strategy whereby he will instrument for schooling with the college-in-the-county dummy variable.

It is worth asking ourselves why the presence of a 4-year college in one’s county would increase schooling. The main reason I can think of is that the presence of the 4-year college increases the likelihood of going to college by lowering the costs, since the student can live at home. This therefore means that we are selecting on a group of compliers whose behavior is affected by the variable. Some kids, in other words, will always go to college regardless of whether a college is in their county, and some will never go despite the presence of the nearby college. But there may exist a group of compliers who go to college only because their county has a college, and if I’m right that this is primarily picking up people going because they can attend while living at home, then it’s necessarily people at some margin who attend only because college became slightly cheaper. This is, in other words, a group of people who are liquidity constrained. And if we believe the returns to schooling for this group are different from those of the always-takers, then our estimates may not represent the ATE. Rather, they would represent the LATE. But in this case, that might actually be an interesting parameter since it gets at the issue of lowering costs of attendance for poorer families.

Here we will do some simple analysis based on Card (1995).

Stata Code

card.do

use https://github.com/scunning1975/mixtape/raw/master/card.dta, clear

* OLS estimate of schooling (educ) on log wages
reg lwage  educ  exper black south married smsa

* 2SLS estimate of schooling (educ) on log wages using "college in the county" as an instrument for schooling
ivregress 2sls lwage (educ=nearc4) exper black south married smsa, first 

* First stage regression of schooling (educ) on all covariates and the college and the county variable
reg educ nearc4 exper black south married smsa

* F test on the excludability of college in the county from the first stage regression.
test nearc4

R Code

card.R

library(AER)
library(haven)
library(tidyverse)

read_data <- function(df)
{
  full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/", 
                     df, sep = "")
  df <- read_dta(full_path)
  return(df)
}

card <- read_data("card.dta")

#Define variable 
#(Y1 = Dependent Variable, Y2 = endogenous variable, X1 = exogenous variable, X2 = Instrument)

attach(card)

Y1 <- lwage
Y2 <- educ
X1 <- cbind(exper, black, south, married, smsa)
X2 <- nearc4

#OLS
ols_reg <- lm(Y1 ~ Y2 + X1)
summary(ols_reg)

#2SLS
iv_reg = ivreg(Y1 ~ Y2 + X1 | X1 + X2)
summary(iv_reg)

Python Code

card.py

import numpy as np 
import pandas as pd 
import statsmodels.api as sm 
import statsmodels.formula.api as smf 
from itertools import combinations 
import plotnine as p

# read data
import ssl
ssl._create_default_https_context = ssl._create_unverified_context
def read_data(file): 
    return pd.read_stata("https://github.com/scunning1975/mixtape/raw/master/" + file)

card = read_data("card.dta")

#OLS
ols_reg = sm.OLS.from_formula("lwage ~ educ + exper + black + south + married + smsa", 
              data = card).fit()

ols_reg.summary()

#2SLS
iv_reg = IV2SLS.from_formula("lwage ~ 1 + exper + black + south + married + smsa + [educ ~ nearc4 ]", card).fit()
iv_reg.summary

Our results from this analysis have been arranged into Table 7.6. First, we report our OLS results. For every one year additional of schooling, respondents’ earnings increase by approximately 7.1%. Next we estimated 2SLS using the ivregress 2sls command in Stata. Here we find a much larger return to schooling than we had found using OLS—around 75% larger in fact. But let’s look at the first stage. We find that the college in the county is associated with 0.327 more years of schooling. This is highly significant (\(p<0.001\)). The \(F\) statistic exceeds 15, suggesting we don’t have a weak instrument problem. The return to schooling associated with this 2SLS estimate is 0.124—that is, for every additional year of schooling, earnings increase by 12.4%. Other covariates are listed if you’re interested in studying them as well.

Table 7.6: OLS and 2SLS regressions of Log Earnings on Schooling

Dependent variable	OLS	2SLS
educ	\(0.071^{***}\)	0.124\(^{**}\)
	(0.003)	(0.050)
exper	\(0.034^{***}\)	0.056\(^{***}\)
	(0.002)	(0.020)
black	\(-0.166^{***}\)	\(-0.116^{**}\)
	(0.018)	(0.051)
south	\(-0.132^{***}\)	\(-0.113^{***}\)
	(0.015)	(0.023)
married	\(-0.036^{***}\)	\(-0.032^{***}\)
	(0.003)	(0.005)
smsa	\(0.176^{***}\)	\(0.148^{***}\)
	(0.015)	(0.031)
First Stage Instrument
College in the county		0.327\(^{***}\)
Robust standard error		(0.082)
F statistic for IV in first stage		15.767
N	3,003	3,003
Mean Dependent Variable	6.262	6.262
Std. Dev. Dependent Variable	0.444	0.444

Standard errors in parenthesis. \(^{*}\) \(p<0.10\), \(^{**}\) \(p<0.05\), \(^{***}\) \(p<0.01\)

Why would the return to schooling be so much larger for the compliers than for the general population? After all, we showed earlier that if this was simply ability bias, then we’d expect the 2SLS coefficient to be smaller than the OLS coefficient, because ability bias implies that the coefficient on schooling is too large. Yet we’re finding the opposite. So a couple of things it could be. First, it could be that schooling has measurement error. Measurement error would bias the coefficient toward zero, and 2SLS would recover its true value. But I find this explanation to be unlikely, because I don’t foresee people really not knowing with accuracy how many years of schooling they currently have. Which leads us to the other explanation, and that is that compliers have larger returns to schooling. But why would this be the case? Assuming that the exclusion restriction holds, then why would compliers, returns be so much larger? We’ve already established that these people are likely being shifted into more schooling because they live with their parents, which suggests that the college is lowering the marginal cost of going to college. All we are left saying is that for some reason, the higher marginal cost of attending college is causing these people to underinvest in schooling; that in fact their returns are much higher.

7.7.2 Fulton Fish Markets

The second exercise that we’ll be doing is based on Graddy (2006). My understanding is that Graddy collected these data herself by recording prices of fish at the actual Fulton Fish Market. I’m not sure if that is true, but I like to believe it’s true. Anyhow, the Fulton Fish Market operated in New York on Fulton Street for 150 years. In November 2005, it moved from Lower Manhattan to a large facility building for the market in the South Bronx. At the time when Graddy (2006) was published, the market was called the New Fulton Fish Market. It’s one of the world’s largest fish markets, second only to the Tsukiji in Tokyo.

Fish are heterogeneous, highly differentiated products. There are anywhere between one hundred and three hundred varieties of fish sold at the market. There are over fifteen varieties of shrimp alone. Within each variety, there’s small fish, large fish, medium fish, fish just caught, fish that have been around a while. There’s so much heterogeneity that customers often want to examine fish personally. You get the picture. This fish market functions just like a two-sided platform matching buyers to sellers, which is made more efficient by the thickness the market produces. It’s not surprising, therefore, that Graddy found the market such an interesting thing to study.

Let’s move to the data. I want us to estimate the price elasticity of demand for fish, which makes this problem much like the problem that Philip Wright faced in that price and quantity are determined simultaneously. The elasticity of demand is a sequence of quantity and price pairs, but with only one pair observed at a given point in time. In that sense, the demand curve is itself a sequence of potential outcomes (quantity) associated with different potential treatments (price). This means the demand curve is itself a real object, but mostly unobserved. Therefore, to trace out the elasticity, we need an instrument that is correlated with supply only. Graddy proposes a few of them, all of which have to do with the weather at sea in the days before the fish arrived to market.

The first instrument is the average maximum wave height in the previous two days. The model we are interested in estimating is:

\[ \begin{align} Q = \alpha + \delta P + \gamma X + \varepsilon \end{align} \]

where \(Q\) is log quantity of whiting sold in pounds, \(P\) is log average daily price per pound, \(X\) are day of the week dummies and a time trend, and \(\varepsilon\) is the structural error term. Table 7.7 presents the results from estimating this equation with OLS (first column) and 2SLS (second column). The OLS estimate of the elasticity of demand is \(-0.549\). It could’ve been anything given price is determined by how many sellers and how many buyers there are at the market on any given day. But when we use the average wave height as the instrument for price, we get a \(-0.96\) price elasticity of demand. A 10% increase in the price causes quantity to decrease by 9.6%. The instrument is strong \((F>22)\). For every one-unit increase in the wave-height, price rose 10%.

Table 7.7: OLS and 2SLS regressions of Log Quantity on Log Price with wave height instrument

Dependent variable	Log(quantity)
	OLS	2SLS
Log(Price)	\(-0.549^{***}\)	\(-0.960^{**}\)
	(0.184)	(0.406)
Monday	\(-0.318\)	\(-0.322\)
	(0.227)	(0.225)
Tuesday	\(-0.684^{***}\)	\(-0.687^{***}\)
	(0.224)	(0.221)
Wednesday	\(-0.535^{**}\)	\(-0.520^{**}\)
	(0.221)	(0.219)
Thursday	0.068	0.106
	(0.221)	(0.222)
Time trend	\(-0.001\)	\(-0.003\)
	(0.003)	(0.003)
First Stage Instrument
Average wave height		\(0.103^{***}\)
Robust standard error		(0.022)
F statistic for IV in first stage		22.638
N	97	97
Mean Dependent Variable	8.086	8.086
Std. Dev. Dependent Variable	0.765	0.765

Standard errors in parenthesis. \(^{*}\) \(p<0.10\), \(^{**}\) \(p<0.05\), \(^{**}\)\(^{*}\) \(p<0.01\)

I suppose the question we have to ask ourselves, though, is what exactly is this instrument doing to supply. What are higher waves doing exactly? They are making it more difficult to fish, but are they also changing the composition of the fish caught? If so, then it would seem that the exclusion restriction is violated because that would mean the wave height is directly causing fish composition to change, which will directly determine quantities bought and sold.

Now let’s look at a different instrument: wind speed (Table 59). Specifically, it’s the three-day lagged maximum wind speed. We present these results in Table 7.7. Here we see something we did not see before, which is that this is a weak instrument. The \(F\) statistic is less than 10 (approximately 6.5). And correspondingly, the estimated elasticity is twice as large as what we found with wave height. Thus, we know from our earlier discussion of weak instruments that this estimate is likely severely biased, and therefore less reliable than the previous one—even though the previous one itself (1) may not convincingly satisfy the exclusion restriction and (2) is at best a LATE relevant to compliers only. But as we’ve said, if we think that the compliers’ causal effects are similar to that of the broader population, then the LATE may itself be informative and useful.

Table 7.8: OLS and 2SLS regressions of Log Quantity on Log Price with windspeed instrument.

Dependent variable	Log(quantity)
	OLS	2SLS
Log Price	\(-0.549^{***}\)	\(-1.960^{**}\)
	(0.184)	(0.873)
Monday	\(-0.318\)	\(-0.332\)
	(0.227)	(0.281)
Tuesday	\(-0.684^{***}\)	\(-0.696^{**}\)
	(0.224)	(0.277)
Wednesday	\(-0.535^{**}\)	\(-0.482^{*}\)
	(0.221)	(0.275)
Thursday	0.068	0.196
	(0.221)	(0.285)
Time trend	\(-0.001\)	\(-0.007\)
	(0.003)	(0.005)
First Stage Instrument
Wind Speed		0.017\(^{**}\)
Robust standard error		(0.007)
F statistic for IV in first stage		6.581
N	97	97
Mean Dependent Variable	8.086	8.086
Std. Dev. Dependent Variable	0.765	0.765

Standard errors in parenthesis. \(^{*}\) \(p<0.10\), \(^{**}\) \(p<0.05\), \(^{**}\)\(^{*}\) \(p<0.01\)

7.8 Popular IV Designs

Instrumental variables is a strategy to adopt when you have a good instrument, and so in that sense, it is a very general design that can be used in just about any context. But over the years, certain types of IV strategies have been used so many times that they constitute their own designs. And from repetition and reflection, we have a better understanding of how these specific IV designs do and do not work. Let’s discuss three such popular designs: the lottery design, the judge fixed effects design, and Bartik instruments.

7.8.1 Lotteries

Previously, we reviewed the use of IV in identifying causal effects when some regressor is endogenous in observational data. But one particular kind of IV application is randomized trials. In many randomized trials, participation is voluntary among those randomly chosen to be in the treatment group. On the other hand, persons in the control group usually don’t have access to the treatment. Only those who are particularly likely to benefit from treatment therefore will probably take up treatment, which almost always leads to positive selection bias. If you compare means between treated and untreated individuals using OLS, you will obtain biased treatment effects even for the randomized trial because of noncompliance. A solution to the problems of least squares in this application is to instrument for Medicaid with whether you were offered treatment and estimate the LATE. Thus even when treatment itself is randomly assigned, it is common for people to use a randomized lottery as an instrument for participation. For a modern example of this, see Baicker et al. (2013), who used the randomized lottery to be enrolled in Oregon’s Medicaid program as an instrument for being on Medicaid. Let’s discuss the Oregon Medicaid studies now, as they are excellent illustrations of the lottery IV design.

What are the effects of expanding access to public health insurance for low-income adults? Are they positive or negative? Are they large or small? Surprisingly, we have not historically had reliable estimates for these very basic questions because we lacked the kind of experiment needed to make claims one way or another. The limited existing evidence was suggestive, with a lot of uncertainty. Observational studies are confounded by selection into health insurance, and the quasi-experimental evidence tended to only focus on the elderly and small children. There has been only one randomized experiment in a developed country, and it was the RAND health insurance experiment in the 1970s. This was an important, expensive, ambitious experiment, but it only randomized cost-sharing—not coverage itself.

But in the 2000s, Oregon chose to expand its Medicaid program for poor adults by making it more generous. Adults aged 19–64 with income less than 100% of the federal poverty line were eligible so long as they weren’t eligible for other similar programs. They also had to be uninsured for fewer than six months and be a legal US resident. The program was called the Oregon Health Plan Standard and it provided comprehensive coverage (but no dental or vision) and minimum cost-sharing. It was similar to other states in payments and management, and the program was closed to new enrollment in 2004.

The expansion is popularly known as the Oregon Medicaid Experiment because the state used a lottery to enroll volunteers. For five weeks, people were allowed to sign up for Medicaid. The state used heavy advertising to make the program salient. There were low barriers to signing up and no eligibility requirements for prescreening. The state in March to October 2008 randomly drew 30,000 people out of a list of 85,000. Those selected were given a chance to apply. If they did apply, then their entire household was enrolled, so long as they returned the application within 45 days. Out of this original 30,000, only 10,000 people were enrolled.

A team of economists became involved with this project early on, out of which several influential papers were written. I’ll now discuss some of the main results from Finkelstein et al. (2012) and Baicker et al. (2013). The authors of these studies sought to study a broad range of outcomes that might be plausibly affected by health insurance—from financial outcomes, to health-care utilization, to health outcomes. The data needed for these outcomes were meticulously collected from third parties. For instance, the pre-randomization demographic information was available from the lottery sign-up. The state administrative records on Medicaid enrollment were also collected and became the primary measure of a first stage (i.e., insurance coverage). And outcomes were collected from administrative sources (e.g., hospital discharge, mortality, credit), mail surveys, and in-person survey and measurement (e.g., blood samples, body mass index, detailed questionnaires).

The empirical framework in these studies is a straightforward IV design. Sometimes they estimated the reduced form, and sometimes they estimated the full 2SLS model. The two-stages were:

\[ \begin{align} \text{INSURANCE}_{ihj} & = \delta_0+\delta_1\text{ LOTTERY}_{ih} + X_{ih}\delta_2 + V_{ih}\delta_3 + \mu_{ihj} \\ y_{ihj} & =\pi_0+\pi_1 I\widehat{\text{NSURANCE}}_{ih} + X_{ih}\pi_2 + V_{ih}\pi_3 + v_{ihj} \end{align} \]

where the first equation is the first stage (insurance regressed onto the lottery outcome plus a bunch of covariates), and the second stage regresses individual-level outcomes onto predicted insurance (plus all those controls). We already know that so long as the first stage is strong, then the F statistic will be large, and the finite sample bias lessens.

The effects of winning the lottery had large effects on enrollment. We can see the results of the first stage in Table 7.9. They used different samples, but the effect sizes were similar. Winning the lottery raised the probability of being enrolled on Medicaid by 26% and raised the number of months of being on Medicaid from 3.3 to 4 months.

Table 7.9: Effect of Lottery on Enrollment

Dependent variable	Full sample	Survey respondents
Ever on Medicaid	0.256	0.290
	(0.004)	(0.007)
Ever on OHP Standard	0.264	0.302
	(0.003)	(0.005)
Number of months on Medicaid	3.355	3.943
	(0.045)	(0.09)

Standard errors in parenthesis.

Across the two papers, the authors looked at the effect of Medicaid’s health insurance coverage on a variety of outcomes including financial health, mortality, and health-care utilization, but I will review only a few here. In Table 7.10, the authors present two regression models: column 2 is the intent to treat estimates, which is the reduced form model, and column 3 is the local average treatment effect estimate, which is our full instrumental variables specification. Interestingly, Medicaid increased the number of hospital admissions but had no effect on emergency room visits. The effect on emergency rooms, in fact, is not significant, but the effect on non-emergency-room admissions is positive and significant. This is interesting because it appears that Medicaid is increasing hospital admission without putting additional strain on emergency rooms, which already have scarce resources.

What other kinds of health-care utilization are we observing in Medicaid enrollees? Let’s look at Table 7.11, which has five health-care utilization outcomes. Again, I will focus on column 3, which is the LATE estimates. Medicaid enrollees were 34% more likely to have a usual place of care, 28% to have a personal doctor, 24% to complete their health-care needs, 20% more likely to get all needed prescriptions and 14% increased satisfaction with the quality of their care.

Table 7.10: Effect of Medicaid on Hospital admission

Dependent variable	ITT	LATE
Any hospital admission	0.5%	2.1%
Hospital admissions through ED	0.2%	0.7%
Hospital admissions not through ED	0.4%	1.6%

Hospital discharge data.

But Medicaid is not merely a way to increase access to health care; it also functions effectively as health care insurance in the event of catastrophic health events. And one of the most widely circulated results of the experiment was the finding that Medicaid had on financial outcomes. In Table 7.12 we see that one of the main effects was reduction in personal debt (by $390) and reducing debt going to debt collection. The authors also found reductions in out-of-pocket medical expenses, and medical expenses, borrowing money or skipping bills for medical expenses, and whether they refused medical treatment due to medical debt.

Table 7.11: Effect of Medicaid on healthcare Usage

Dependent variable	ITT	LATE
Have a usual place of care	9.9%	33.9%
Have a personal doctor	8.1%	28.0%
Got all needed healthcare	6.9%	23.9%
Got all needed prescriptions	5.6%	19.5%
Satisfied with quality of care	4.3%	14.2%

Standard errors in parenthesis.

Table 7.12: Effect of Medicaid on Hospital admission

Dependent variable	ITT	LATE
Had a bankruptcy	0.2%	0.9%
Had a collection	\(-1.2\%\)	\(-4.8\%\)
Had a medical collection	\(-1.6\%\)	\(-6.4\%\)
Had non-medical collection	\(-0.5\%\)	\(-1.8\%\)
$ owed medical collection	\(-\$99\)	\(-\$390\)

Credit records.

But the effect on health outcomes was a little unclear from this study. The authors find self-reported health outcomes to be improving, as well as a reduction in depression. They also find more healthy physical and mental health days. But the effects are overall small. Furthermore, they ultimately do not find that Medicaid had any effect on mortality—a result we will return to again in the difference-in-differences chapter.

In conclusion, we see a powerful use of IV in the assignment of lotteries to recipients. The lotteries function as instruments for treatment assignment, which can then be used to estimate some local average treatment effect. This is incredibly useful in experimental designs if only because humans often refuse to comply with their treatment assignment or even participate in the experiment altogether!

Table 7.13: Effect of Medicaid on Hospital admission

Dependent variable	ITT	LATE
Health good, very good, or excellent	3.9%	13.3%
Health stable or improving	3.3%	11.3%
Depression screen NEGATIVE	2.3%	7.8%
CDC healthy days (physical)	0.381	1.31
CDC healthy days (mental)	0.603	2.08

7.8.2 Judge fixed effects

A second IV design that has become extremely popular in recent years is the “judge fixed effects” design. You may also hear it called the “leniency design,” but because the applications so often involve judges, it seems the former name has stuck. A search on Google Scholar for the term yields over 70 hits, with over 50 since 2018 alone.

The concept of the judge fixed effects design is that there exists a narrow pipeline through which all individuals must pass, numerous randomly assigned decision-makers blocking the individuals’ passage who assign a treatment to the individuals and discretion among the decision-makers. When all three are there, you probably have the makings of a judge fixed effects design. The reason the method is called the judge fixed effects design is because it has traditionally exploited a feature in American jurisprudence where jurisdictions will randomly assign judges to defendants. In Harris County, Texas, for instance, they used to use a bingo machine to assign defendants to one of dozens of courts (Mueller-Smith 2015).

Figure 7.7: Randomized judge assignment. Although justice is supposedly blind, judges are complex bundles of characteristics that affect their judgments. Artwork by Seth.

The first paper to recognize that there were systematic differences in judge sentencing behavior was an article by Gaudet, Harris, and John (1933). The authors were interested in better understanding what, other than guilt, determined the sentencing outcomes of defendants. They decided to focus on the judge in part because judges were being randomly rotated to defendants. And since they were being “by chance” rotated to defendants, in a large sample, the characteristics of the defendants should’ve remained approximately the same across all judges. Any differences in sentencing outcomes, therefore, wouldn’t be because of the underlying charge or even the defendant’s guilt, but rather, would be connected to the judge. See Figure 7.7 for a beautiful drawing of this identification strategy based on over 7,000 hand collected cases showing systematic differences in judge sentencing behavior.

Figure 7.8: Variation in judge sentencing outcomes. This figure originally appeared in Gaudet, Harris, and John (1933). Reprinted by special permission of Northwestern University Pritzker School of Law, Journal of Criminal Law and Criminology

Figure 7.8 is a pretty typical graphic for any paper on judge fixed effects showing the variation in the judge’s propensities; it’s just kind of interesting that it appears from the very beginning back in 1933. And as you can see in Figure 7.8, there is weirdly enough a lot of variation in the sentencing propensities across the six judges. Judge 2 imposed imprisonment in only 33.6% of his cases, whereas Judge 4 imposed imprisonment in a whopping 57.7%. And since they are all seeing on average the same defendants, it can’t be that Judge 4 is simply seeing worse cases. Rather, there appears to be something systematic, like a tendency for certain judges to always judge defendants more harshly. But why are they like this? Gaudet, Harris, and John (1933) offer the following conjecture:

Perhaps the most interesting thing to be noticed in these graphs is the fact that the sentencing tendency of the judge seems to be fairly well determined before he sits on the bench. In other words what determines whether a judge will be severe or lenient is to be found in the environment to which the judge has been subjected previous to his becoming an administrator of sentences.

But the main takeaway is that the authors were the first to discover that the leniency or severity of the judge, and not merely the defendant’s own guilt, plays a significant role apparently in the final determination of a case against the defendant. The authors write:

The authors wish to point out that these results tend to show that some of our previous studies in the fields of criminology and penology are based upon very unreliable evidence if our results are typical of sentencing tendencies. In other words, what type of sentence received by a prisoner may be either an indication of the seriousness of his crime or of the severity of the judge. (p.815)

The next mention of the explicit judge fixed effects design is in the Imbens and Angrist (1994) article decomposing IV into the LATE parameter using potential outcomes notation. At the conclusion of their article, they provide three examples of IV designs that may or may not fit the five identifying assumptions of IV that I discussed earlier. They write:

Example 2 (Administrative Screening): Suppose applicants for a social program are screened by two officials. The two officials are likely to have different admission rates, even if the stated admission criteria are identical. Since the identity of the official is probably immaterial to the response, it seems plausible that Condition 1 independence is satisfied. The instrument is binary so Condition 3 is trivially satisfied. However, Condition 2 monotonicity requires that if official \(A\) accepts applicants with probability \(P(0)\), and official B accepts people with probability \((P1)>P(0)\), official B must accept any applicant who would have been accepted by official \(A\). This is unlikely to hold if admission is based on a number of criteria. Therefore, in this example we cannot use Theorem 1 to identify a local average treatment effect nonparametrically despite the presence of an instrument satisfying Condition 1 independence. (p.472)

While the first time we see the method used for any type of empirical identification is Waldfogel (1995), the first explicit IV strategy is a paper ten years later by Kling (2006), who used randomized judge assignment with judge propensities to instrument for incarceration length. He then linked defendants to employment and earnings records, which he then used to estimate the causal effect of incarceration on labor-market outcomes. He ultimately finds no adverse effects on labor-market consequences from longer sentences in the two states he considers.

But this question was revisited by Mueller-Smith (2015), who used Harris County, Texas, for his location. Harris County has dozens of courts and defendants are randomly assigned to one of them. Mueller-Smith linked defendant outcomes to a variety of labor-market and criminal outcomes, and came to the opposite conclusion as Kling (2006). Mueller-Smith (2015) finds that incarceration generates net increases in the frequency and severity of recidivism, worsens labor-market outcomes, and increases defendant’s dependence on public assistance.

Judicial severity causing adverse consequences on defendants is practically a hallmark of the judge fixed effects literature. Just to name a few such examples, there is the finding that less allowance of Chapter 13 bankruptcy worsens future financial events (Dobbie, Goldsmith-Pinkham, and Yang 2017), racial bias among bail judges (Arnold, Dobbie, and Yang 2018), pretrial detention having higher rates of guilty pleas, conviction, recidivism, and worsened labor-market outcomes (Leslie and Pope 2018; Dobbie, Goldin, and Yang 2018; Stevenson 2018), juvenile incarceration worsening high school outcomes and adult recidivism rates (Aizer and Doyle 2015), foster care raising juvenile delinquency, teen pregnancy, and worsening future employment (Doyle 2007), foster care increasing adult crime (Doyle 2008), and countless others. But there are a few exceptions. For instance, Norris, Pecenco, and Weaver (2020) find beneficial effects to children when the marginal siblings and parents are incarcerated.

The three main identifying assumptions that should be on the researcher’s mind when attempting to implement a judge fixed effects design are the independence assumption, exclusion restriction, and the monotonicity assumption. Let’s discuss them each at a time because, in some scenarios, one of these may be more credible than the other.

The independence assumption seems to be satisfied in many cases because the administrators in question are literally being randomly assigned to individual cases. As such, our instrument—which is sometimes modeled as the average propensity of the judge excluding the case in question or simply as a series of judge fixed effects (which, as I’ll mention in a moment, turns out to be equivalent)—easily passes the independence test. But it’s possible that strategic behavior on the part of the defendant in response to the strictness of the judge they were assigned can undermine the otherwise random assignment. Consider something that Gaudet, Harris, and John (1933) observed in their original study regarding the dynamics of the courtroom when randomly assigned a severe judge:

The individual tendencies in the sentencing tendencies of judges are evidently recognized by many who are accustomed to observe this sentencing. The authors have been told by several lawyers that some recidivists know the sentencing tendencies of judges so well that the accused will frequently attempt to choose which judge is to sentence them, and further, some lawyers say that they are frequently able to do this. It is said to be done in this way. If the prisoner sees that he is going to be sentenced by Judge X, whom he believes to be severe in his sentencing tendency, he will change his plea from “Guilty” to “Non Vult” or from “Non Vult” to “Not Guilty,” etc. His hope is that in this way the sentencing will be postponed and hence he will probably be sentenced by another judge. (p.812)

There are several approaches one can take to assessing independence. First, checking for balance on pre-treatment covariates is an absolute must. Insofar as this is a randomized experiment, then all observable and unobservable characteristics will be distributed equally across the judges. While we cannot check for balance on unobservables, we can check for balance on observables. Most papers of which I am aware check for covariate balance, usually before doing any actual analysis.

Insofar as you suspect endogenous sorting, you might simply use the original assignment, not the final assignment, for identification. This is because in most cases, we will know the initial judge assignment was random. But this approach may not be feasible in many settings if initial judge or court assignment is not available. Nevertheless, endogenous sorting in response to the severity of the judge could undermine the design by introducing a separate mechanism by which the instrument impacts the final decision (via sorting into the lenient judge’s courtroom if possible), and the researcher should attempt to ascertain through conversations with administrators the degree to which this practically occurs in the data.

The violation of exclusion is more often the worry, though, and really should be evaluated case by case. For instance, in Dobbie, Goldin, and Yang (2018), the authors are focused on pretrial detention. But pretrial detention is determined by bail set by judges who do not themselves have any subsequent interaction with the next level’s randomized judge, and definitely don’t have any interaction with the defendant upon the judicial ruling and punishment rendered. So in this case, it does seem like Dobbie, Goldin, and Yang (2018) might have a more credible argument that exclusion holds.

But consider a situation where a defendant is randomly assigned a severe judge. In expectation, if the case goes to trial, the defendant faces a higher expected penalty even given a fixed probability of conviction across any judge for no other reason than that the stricter judge will likely choose a harsher penalty and thus drive up the expected penalty. Facing this higher expected penalty, the defense attorney and defendant might decide to accept a lesser plea in response to the judge’s anticipated severity, which would violate exclusion since exclusion requires the instrument effect the outcome only through the judge’s decision (sentence).

But even if exclusion can be defended, in many situations monotonicity becomes the more difficult case to make for this design. It was explicitly monotonicity that made Imbens and Angrist (1994) skeptical that judge fixed effects could be used to identify the local average treatment effect. This is because the instrument is required to weakly operate the same across all defendants. Either a judge is strict or she isn’t, but she can’t be both in different circumstances. Yet humans are complex bundles of thoughts and experiences, and those biases may operate in non-transitive ways. For instance, a judge may be lenient, except when the defendant is black or if the offense is a drug charge, in which case they switch and become strict. Mueller-Smith (2015) attempted to overcome potential violations of exclusion and monotonicity through a parametric strategy of simultaneously instrumenting for all observed sentencing dimensions and thus allowing the instruments’ effect on sentencing outcomes to be heterogeneous in defendant traits and crime characteristics.

Formal solutions to querying the plausibility of these assumptions have appeared in recent years, though. Frandsen, Lefgren, and Leslie (2019) propose a test for exclusion and monotonicity based on relaxing the monotonicity assumption. This test requires that the average treatment effect among individuals who violate monotonicity be identical to the average treatment effect among some subset of individuals who satisfy it. Their test simultaneously tests for exclusion and monotonicity, so one cannot be sure which violation is driving the test’s result unless theoretically one rules out one of the two using a priori information. Their proposed test is based on two observations: that the average outcomes, conditional on judge assignment, should fit a continuous function of judge propensities, and secondly, the slope of that continuous function should be bounded in magnitude by the width of the outcome variable’s support. The test itself is relatively straightforward and simply requires examining whether observed outcomes averaged by judges are consistent with such a function. We can see a picture of what it looks like to pass this test in the top panel of Figure 7.9 versus the bottom panel, which fails the test.

Figure 7.9: Average outcomes as a function of judge propensities. Reprinted from Frandsen, Lefgren, and Leslie (2019).

While the authors have made available code and documentation that can be used to implement this test,¹⁹ it is not currently available in R and therefore will not be reviewed here.

In this section, I’d like to accomplish two things. First, I’d like to review an interesting new paper by Megan Stevenson that examined how cash bail affected case outcomes (Stevenson 2018). As this is an important policy question, I felt it would be good to review this excellent study. But the second purpose of this section is to replicate her main results so that the reader can see exactly how to implement this instrumental variables strategy.

As with most judge fixed effects papers, Stevenson is working with administrative data for a large city. Large cities are probably the best context due to the large samples which can help ameliorate the finite sample bias of IV. Fortunately, these data are often publicly available and need only be scraped from court records that are in many locations posted online. Stevenson (2018) focuses on Philadelphia, where the natural experiment is the random assignment of bail judges (“magistrates”) who unsurprisingly differ widely in their propensity to set bail at affordable levels. In other words, bail judges differ systematically in the price they set for bail, and given a downward-sloping demand curve, more severe judges setting expensive bails will see more defendants unable to pay their bail. As a result, they are forced to remain in detention prior to the trial.

Using a variety of IV estimators, Stevenson (2018) finds that an increase in randomized pretrial detention leads to a 13% increase in the likelihood of receiving a conviction. She argues that this is caused by an increase in guilty pleas among defendants who otherwise would have been acquitted or had their charges dropped—a particularly problematic mechanism, if true. Pretrial detention also led to a 42% increase in the length of the incarceration sentence and a 41% increase in the amount of non-bail fees owed. This provides support for idea that cash bail contributes to a cycle of poverty in which defendants unable to pay their court fees end up trapped in the penal system through higher rates of guilt, higher court fees, and likely higher rates of reoffending (Dobbie, Goldin, and Yang 2018).

One might think that the judge fixed effects design is a “just identified” model. Can’t we just use as our instrument the average strictness for each judge (excluding the defendant’s own case)? Then we have just one instrument for our one endogenous variable, and 2SLS seems like a likely candidate, right? After all, that one instrument would be unique to each individual because each individual would have a unique judge and a unique average strictness if average strictness was calculated as the mean of all judge sentencing excluding the individual under consideration.

The problem is that this is still just a high-dimension instrument. The correct specification is to use the actual judge fixed effects, and depending on your application you may have anywhere from eight (as in Stevenson’s case) to hundreds of judges. Insofar as some of these are weak, which they probably will be, you run into a typical kind of overidentification problem where in finite samples you begin moving the point estimates back to centering on the OLS bias as I discussed earlier. This issue is still being resolved by econometricians and is likely to be an active area of research going forward. Some solutions may be to use high-dimension reduction techniques such as LASSO (Gilchrist and Sands 2016), instrument selection (Donald and Newey 2001), or perhaps combining individual judges with similar strictness into only one instrument.

Let’s now look at data from Stevenson (2018) itself. Stevenson’s data contains 331,971 observations and eight randomly assigned bail judges. Like many papers in the judge fixed effects literature, she uses the jackknife instrumental variables estimator (JIVE) (Angrist, Imbens, and Krueger 1999). While 2SLS is the most commonly used IV estimator in applied microeconomics applications, it suffers from finite sample problems when there are weak instruments and the use of many instruments as we showed with the discussion of Bound, Jaeger, and Baker (1995). Angrist, Imbens, and Krueger (1999) proposed an estimator that attempts to eliminate the finite-sample bias of 2SLS called JIVE.²⁰ These aren’t perfect, as their distributions are larger than that of the 2SLS estimator, but they may have an advantage when there are several instruments and some of which are weak (as is likely to occur with judge fixed effects).

JIVE is popularly known as a “leave one out” estimator. Angrist, Imbens, and Krueger (1999) suggest using all observations in this estimator except for the \(i\) unit. This is the nice feature for judge fixed effects because ideally the instrument is the mean strictness of the judge in all other cases, excluding the particular defendant’s case. So JIVE is nice both for its handling of the finite sample bias, and for its construction of the theoretical instrument more generally.

Given the econometrics of judge fixed effects with its many instruments is potentially the frontier of econometrics, my goal here will be somewhat backwards looking. We will simply run through some simple exercises using JIVE so that you can see how historically researchers are estimating their models.

Stata Code

bail.do

use https://github.com/scunning1975/mixtape/raw/master/judge_fe.dta, clear
 
global judge_pre judge_pre_1 judge_pre_2 judge_pre_3 judge_pre_4 judge_pre_5 judge_pre_6 judge_pre_7 judge_pre_8
global demo black age male white 
global off      fel mis sum F1 F2 F3 F M1 M2 M3 M 
global prior priorCases priorWI5 prior_felChar  prior_guilt onePrior threePriors
global control2     day day2 day3  bailDate t1 t2 t3 t4 t5 t6


* Naive OLS
* minimum controls
reg guilt jail3 $control2, robust
* maximum controls
reg guilt jail3 possess robbery DUI1st drugSell aggAss $demo $prior $off  $control2 , robust


* First stage
reg jail3 $judge_pre $control2, robust
reg jail3 possess robbery DUI1st drugSell aggAss $demo $prior $off  $control2 $judge_pre, robust



** Instrumental variables estimation
* 2sls main results
* minimum controls
ivregress 2sls guilt (jail3= $judge_pre) $control2, robust first
* maximum controls
ivregress 2sls guilt (jail3= $judge_pre) possess robbery DUI1st drugSell aggAss $demo $prior $off $control2 , robust first

* JIVE main results
* jive can be installed using: net from https://www.stata-journal.com/software/sj6-3/
* net install st0108

* minimum controls
jive guilt (jail3= $judge_pre) $control2, robust
* maximum controls
jive guilt (jail3= $judge_pre) possess robbery DUI1st drugSell aggAss $demo $prior $off $control2 , robust

R Code

bail.R

library(tidyverse)
library(haven)
library(estimatr)
library(lfe)
library(SteinIV)

read_data <- function(df)
{
  full_path <- paste("https://github.com/scunning1975/mixtape/raw/master/", 
                     df, sep = "")
  df <- read_dta(full_path)
  return(df)
}

judge <- read_data("judge_fe.dta")

#grouped variable names from the data set
judge_pre <- judge %>% 
  select(starts_with("judge_")) %>% 
  colnames() %>% 
  subset(., . != "judge_pre_8") %>% # remove one for colinearity
  paste(., collapse = " + ")

demo <- judge %>% 
  select(black, age, male, white) %>% 
  colnames() %>% 
  paste(., collapse = " + ")

off <- judge %>% 
  select(fel, mis, sum, F1, F2, F3, M1, M2, M3, M) %>% 
  colnames() %>% 
  paste(., collapse = " + ")

prior <- judge %>% 
  select(priorCases, priorWI5, prior_felChar, 
         prior_guilt, onePrior, threePriors) %>% 
  colnames() %>% 
  paste(., collapse = " + ")

control2 <- judge %>%
  mutate(bailDate = as.numeric(bailDate)) %>% 
  select(day, day2, bailDate, 
         t1, t2, t3, t4, t5) %>% # all but one time period for colinearity
  colnames() %>% 
  paste(., collapse = " + ")

#formulas used in the OLS
min_formula <- as.formula(paste("guilt ~ jail3 + ", control2))
max_formula <- as.formula(paste("guilt ~ jail3 + possess + robbery + DUI1st + drugSell + aggAss",
                                demo, prior, off, control2, sep = " + "))

#max variables and min variables
min_ols <- lm_robust(min_formula, data = judge)
max_ols <- lm_robust(max_formula, data = judge)

#--- Instrumental Variables Estimations
#-- 2sls main results
#- Min and Max Control formulas
min_formula <- as.formula(paste("guilt ~ ", control2, " | 0 | (jail3 ~ 0 +", judge_pre, ")"))
max_formula <- as.formula(paste("guilt ~", demo, "+ possess +", prior, "+ robbery +", 
                                off, "+ DUI1st +", control2, "+ drugSell + aggAss | 0 | (jail3 ~ 0 +", judge_pre, ")"))
#2sls for min and max
min_iv <- felm(min_formula, data = judge)
summary(min_iv)
max_iv <- felm(max_formula, data = judge)
summary(max_iv)



#-- JIVE main results
#- minimum controls
y <- judge %>%
  pull(guilt)

X_min <- judge %>%
  mutate(bailDate = as.numeric(bailDate)) %>%
  select(jail3, day, day2, t1, t2, t3, t4, t5, bailDate) %>%
  model.matrix(data = .,~.)

Z_min <- judge %>%
  mutate(bailDate = as.numeric(bailDate)) %>%
  select(-judge_pre_8) %>%
  select(starts_with("judge_pre"), day, day2, t1, t2, t3, t4, t5, bailDate) %>%
  model.matrix(data = .,~.)

jive.est(y = y, X = X_min, Z = Z_min)

#- maximum controls
X_max <- judge %>%
  mutate(bailDate = as.numeric(bailDate)) %>%
  select(jail3, white, age, male, black,
         possess, robbery, prior_guilt,
         prior_guilt, onePrior, priorWI5, prior_felChar, priorCases,
         DUI1st, drugSell, aggAss, fel, mis, sum,
         threePriors,
         F1, F2, F3,
         M, M1, M2, M3,
         day, day2, bailDate, 
         t1, t2, t3, t4, t5) %>%
  model.matrix(data = .,~.)

Z_max <- judge %>%
  mutate(bailDate = as.numeric(bailDate)) %>%
  select(-judge_pre_8) %>%
  select(starts_with("judge_pre"), white, age, male, black,
         possess, robbery, prior_guilt,
         prior_guilt, onePrior, priorWI5, prior_felChar, priorCases,
         DUI1st, drugSell, aggAss, fel, mis, sum,
         threePriors,
         F1, F2, F3,
         M, M1, M2, M3,
         day, day2, bailDate, 
         t1, t2, t3, t4, t5) %>%
  model.matrix(data = .,~.)

jive.est(y = y, X = X_max, Z = Z_max)

Python Code

bail.py

import numpy as np 
import pandas as pd 
import statsmodels.api as sm 
import statsmodels.formula.api as smf 
from itertools import combinations 
import plotnine as p

# read data
import ssl
ssl._create_default_https_context = ssl._create_unverified_context
def read_data(file): 
    return pd.read_stata("https://github.com/scunning1975/mixtape/raw/master/" + file)


judge = read_data("judge_fe.dta")
judge['bailDate'] = (judge['bailDate'] - pd.to_datetime('1970-01-01')).dt.days.values

# grouped variable names from the data set
judge_pre = "+".join(judge.columns[judge.columns.str.contains('^judge_pre_[1-7]')])
demo = "+".join(['black', 'age', 'male', 'white'])
off = "+".join(['fel', 'mis', 'sum', 'F1', 'F2', 'F3', 'M1', 'M2', 'M3', 'M'])
prior = "+".join(['priorCases', 'priorWI5', 'prior_felChar', 'prior_guilt', 'onePrior', 'threePriors'])
control2 = "+".join(['day', 'day2', 'bailDate', 't1', 't2', 't3', 't4', 't5'])

#formulas used in the OLS
min_formula = "guilt ~ jail3 + " + control2
max_formula = """guilt ~ jail3 + possess + robbery + DUI1st + drugSell + 
                aggAss + {demo} + {prior} + {off} + {control2}""".format(demo=demo,
                                                                        prior=prior,
                                                                        off=off,
                                                                        control2=control2)

#max variables and min variables
min_ols = sm.OLS.from_formula(min_formula, data = judge).fit()
max_ols = sm.OLS.from_formula(max_formula, data = judge).fit()
print("OLS")
Stargazer([min_ols, max_ols])



#--- Instrumental Variables Estimations
#-- 2sls main results
#- Min and Max Control formulas

min_formula = "guilt ~ {control2} + [jail3 ~ {judge_pre}]".format(control2=control2, judge_pre=judge_pre)
max_formula = """guilt ~ {demo} + possess + {prior} + robbery + {off} + DUI1st + {control2} + drugSell + aggAss +
                    [jail3 ~ {judge_pre}]""".format(demo=demo,
                                                    prior=prior,
                                                    off=off,
                                                    control2=control2,
                                                   judge_pre=judge_pre)

min_iv = IV2SLS.from_formula(min_formula, data = judge).fit()
max_iv = IV2SLS.from_formula(max_formula, data = judge).fit()


print("IV")
min_iv.summary
max_iv.summary


#-- JIVE main results
#- minimum controls

from rpy2 import robjects
from rpy2.robjects import pandas2ri
from rpy2.robjects.packages import importr
pandas2ri.activate()
SteinIV = importr('SteinIV')

y = judge['guilt']
X_min = judge[['jail3', 'day', 'day2', 't1', 't2', 't3', 't4', 't5', 'bailDate']]
X_min['intercept'] = 1

Z_min = judge[judge_pre.split('+') + ['day', 'day2', 't1', 't2', 't3', 't4', 't5', 'bailDate']]
Z_min['intercept'] = 1


y = robjects.globalenv['y'] = y
X_min = robjects.globalenv['X_min'] = np.array(X_min)
Z_min = robjects.globalenv['Z_min'] = np.array(Z_min)

SteinIV.jive_est(y = y, X=X_min, Z=Z_min)

#- maximum controls
X_max = judge[['jail3', 'white', 'age', 'male', 'black',
         'possess', 'robbery', 
         'prior_guilt', 'onePrior', 'priorWI5', 'prior_felChar', 'priorCases',
         'DUI1st', 'drugSell', 'aggAss', 'fel', 'mis', 'sum',
         'threePriors',
         'F1', 'F2', 'F3',
         'M', 'M1', 'M2', 'M3',
         'day', 'day2', 'bailDate', 
         't1', 't2', 't3', 't4', 't5']]
X_max['intercept'] = 1

Z_max = judge[judge_pre.split('+') + ['white', 'age', 'male', 'black',
         'possess', 'robbery', 
         'prior_guilt', 'onePrior', 'priorWI5', 'prior_felChar', 'priorCases',
         'DUI1st', 'drugSell', 'aggAss', 'fel', 'mis', 'sum',
         'threePriors',
         'F1', 'F2', 'F3',
         'M', 'M1', 'M2', 'M3',
         'day', 'day2', 'bailDate', 
         't1', 't2', 't3', 't4', 't5']]
Z_max['intercept'] = 1
X_max = robjects.globalenv['X_max'] = np.array(X_max)
Z_max = robjects.globalenv['Z_max'] = np.array(Z_max)


SteinIV.jive_est(y = y, X = X_max, Z = Z_max)

These results are pretty interesting. Notice that if we just were to examine this using OLS, you’d conclude there was actually no connection between pre-trial detention and a guilty plea. It was either zero using only time controls, or it raised the probability 3% with our fuller set of controls (mainly demographic controls, prior offenses, and the characteristics of the offense itself). But, when we use IV with the binary judge fixed effects as instruments, the effects change a lot. We end up with estimates ranging from 15 to 21%, and of these probably we should be more focused on JIVE because of its advantages, as previously mentioned. You can examine the strength of the instruments yourself by regressing detention onto the binary instruments to see just how strong the instruments are, but they are very strong. All but two are statistically significant at the 1% level. Of the other two, one has a p-value of 0.076 and the other is weak \((p<0.25)\).

Table 7.14: OLS and IV Estimates of Detention on Guilty Plea

Model:	OLS		2SLS		JIVE
Detention	-0.001	0.029\(^{***}\)	0.151\(^{**}\)	0.186\(^{***}\)	0.162\(^{**}\)	0.212\(^{***}\)
	(0.002)	(0.002)	(0.065)	(0.064)	(0.070)	(0.076)
N	331,971	331,971	331,971	331,971	331,971	331,971
Mean guilt	0.49	0.49	0.49	0.49	0.49	0.49

First model includes controls for time; second model controls for characteristics of the defendant. Outcome is guilty plea. Heteroskedastic robust standard errors in parenthesis. \(^{*}\) \(p<0.10\), \(^{**}\) \(p<0.05\), \(^{***}\) \(p<0.01\)

The judge fixed effects design is a very popular form of instrumental variables. It is used whenever there exists a wheel of randomly assigned decision makers assigning a treatment of some kind to other people. Important questions and answers in the area of criminal justice have been examined using this design. When linked with external administrative data sources, researchers have been able to more carefully evaluate the causal effect of criminal justice interventions on long-term outcomes. But the procedure has uniquely sensitive identifying assumptions related to independence, exclusion, and monotonicity that must be carefully contemplated before going forward with the design. Nevertheless, when those assumptions can be credibly defended, it is a powerful estimator of local average treatment effects.

7.8.3 Bartik instruments

Bartik instruments, also known as shift-share instruments, were named after Timothy Bartik, who used them in a careful study of regional labor-markets (Bartik 1991). Both Bartik’s book and the instrument received wider attention the following year with Blanchard and Katz (1992). It has been particularly influential in the areas of migration and trade, as well as labor, public, and several other fields. A simple search for the phrase “Bartik instrument” on Google Scholar reveals almost five hundred cites at the time of this writing.

But just as Stigler’s law of eponymy promises (Stigler 1980), Bartik instruments do not originate with Bartik (1991). Goldsmith-Pinkham, Sorkin, and Swift (2020) notes that traces of it can be found as early as Perloff (1957) who showed that industry shares could be used to predict income levels. Freeman (1980) also used the change in industry composition as an instrument for labor demand. But due to Bartik’s careful empirical analysis using the instrument combined with his detailed exposition of the logic of how the national growth shares created variation in labor-market demand in Appendix 4 of his book, the design has been named after him.

OLS estimates of the effect of employment growth rates on labor-market outcomes are likely hopelessly biased since labor-market outcomes are simultaneously determined by labor supply and labor demand. Bartik therefore suggested using IV to resolve the issue and in Appendix 4 describes the ideal instrument.

Obvious candidates for instruments are variables shifting MSA labor demand. In this book, only one type of demand shifter is used to form instrumental variables: the share effect from a shift-share analysis of each metropolitan area and year-to-year employment change. A shift-share analysis decomposes MSA growth into three components: a national growth component, which calculates what growth would have occurred if all industries in the MSA had grown at the all-industry national average; a share component, which calculates what extra growth would have occurred if each industry in the MSA had grown at that industry’s national average; and a shift component, which calculates the extra growth that occurs because industries grow at different rates locally than they do nationally. Bartik (1991)

Summarizing all of this, the idea behind a Bartik instrument is to measure the change in a region’s labor demand due to changes in the national demand for different industries’ products.²¹ To make this concrete, let’s assume that we are interested in estimating the following wage equation:

\[ \begin{align} Y_{l,t} = \alpha + \delta I_{l,t} + \rho X_{l,t} + \varepsilon_{l,t} \end{align} \]

where \(Y_{l,t}\) is log wages in location \(l\) (e.g., Detroit) in time period \(t\) (e.g., 2000) among native workers, \(I_{l,t}\) are immigration flows in region \(l\) at time period \(t\) and \(X_{l,t}\) are controls that include region and time fixed effects, among other things. The parameter \(\delta\) as elsewhere is some average treatment effect of the immigration flows’ effect on native wages. The problem is that it is almost certainly the case that immigration flows are highly correlated with the disturbance term such as the time-varying characteristics of location \(l\) (e.g., changing amenities) (Sharpe 2019).

The Bartik instrument is created by interacting initial “shares” of geographic regions, prior to the contemporaneous immigration flow, with national growth rates. The deviations of a region’s growth from the US national average are explained by deviations in the growth prediction variable from the US national average. And deviations of the growth prediction variables from the US national average are due to the shares because the national growth effect for any particular time period is the same for all regions. We can define the Bartik instrument as follows:

\[ \begin{align} {B}_{l,t} = \sum_{k=1}^K z_{l,k,t^0} m_{k,t} \end{align} \]

where \(z_{l,k,t^0}\) are the “initial” \(t^0\) share of immigrants from source country \(k\) (e.g., Mexico) in location \(l\) (e.g., Detroit) and \(m_{k,t}\) is the change in immigration from country \(k\) (e.g., Mexico) into the US as a whole. The first term is the share variable and the second term is the shift variable. The predicted flow of immigrants, \({B}\), into destination \(l\) (e.g., Detroit) is then just a weighted average of the national inflow rates from each country in which weights depend on the initial distribution of immigrants.

Once we have constructed our instrument, we have a two-stage least squares estimator that first regresses the endogenous \(I_{l,t}\) onto the controls and our Bartik instrument. Using the fitted values from that regression, we then regress \(Y_{l,t}\) onto \(\widehat{I}_{l,t}\) to recover the impact of immigration flows onto log wages.

7.8.4 Shifts vs Shares

I’d like to now turn to the identifying assumptions that are unique to this design. There are two perspectives as to what is needed to leverage a Bartik design to identify a causal effect and they separately address the roles of the exogeneity of the shares versus the shifts. Which perspective you take will depend on the ex ante plausibility of certain assumptions. They will also depend on different tools.

Goldsmith-Pinkham, Sorkin, and Swift (2020) explain the shares perspective. They show that while the shifts affect the strength of the first stage, it is actually the initial shares that provide the exogenous variation. They write that “the Bartik instrument is ‘equivalent’ to using local industry shares as instruments, and so the exogeneity condition should be interpreted in terms of the shares.” Insofar as a researcher’s application is exploiting differential exogenous exposure to common shocks, industry specific shocks, or a two-industry scenario, then it is likely that the source of exogeneity comes from the initial shares and not the shifts. This is a type of strict exogeneity assumption where the initial shares are exogenous conditional on observables, such as location fixed effects. What this means in practice is that the burden is on the researcher to argue why they believe the initial shares are indeed exogenous.

But while exogenous shares are sufficient, it turns out they are not necessary for identification of causal effects. Temporal shocks may provide exogeous sources of variation. Borusyak, Hull, and Jaravel (2019) explain the shifts perspective. They show that exogenous independent shocks to many industries allow a Bartik design to identify causal effects regardless of whether the shares are exogenous so long as the shocks are uncorrelated with the bias of the shares. Otherwise, it may be the shock itself that is creating exogenous variation, in which case the focus on excludability moves away from the initial shares and more towards the national shocks themselves (Borusyak, Hull, and Jaravel 2019). The authors write:

Ultimately, the plausibility of our exogenous shocks framework, as with the alternative framework of Goldsmith-Pinkham, Sorkin, and Swift (2020) based on exogenous shares, depends on the shift-share IV application. We encourage practitioners to use shift-share instruments based on an a priori argument supporting the plausibility of either one of these approaches; various diagnostics and tests of the framework that is most suitable for the setting may then be applied. While Borusyak, Hull, and Jaravel (2019) develops such procedures for the “shocks” view, Goldsmith-Pinkham, Sorkin, and Swift (2020) provide different tools for the “shares” view.

Insofar as we think about the initial shares as the instruments, and not the shocks, then we are in a world in which those initial shares are measuring differential exogenous exposures to some common shock. As the shares are equilibrium values, based on past labor supply and demand, it may be tough to justify why we should consider them exogenous to the structural unobserved determinants of some future labor-market outcome. But it turns out that that is not the critical piece. A valid Bartik design can be valid even if the shares are correlated indirectly with the levels of the outcomes; they just can’t be correlated with the differential changes associated with the national shock itself, which is a subtle but distinct point.

One challenge with Bartik instruments is the sheer number of shifting values. For instance, there are almost four hundred different industries in the United States. Multiplied over many time periods and the exclusion restriction becomes a bit challenging to defend. Goldsmith-Pinkham, Sorkin, and Swift (2020) provide several suggestions for evaluating the central identifying assumption in this design. For instance, if there is a pre-period, then ironically this design begins to resemble the difference-in-differences design that we will discuss in a subsequent chapter. In that case, we might test for placebos, pre-trends, and so forth.

Another possibility is based on the observation that the Bartik instrument is simply a specific combination of many instruments. In that sense, it bears some resemblance to the judge fixed effects design from earlier in which the judge’s propensity was itself a specific combination of many binary fixed effects. With many instruments, other options become available. If the researcher is willing to assume a null of constant treatment effects, then overidentification tests are an option. But overidentification tests can fail if there is treatment heterogeneity as opposed to exclusion not holding. Similar to Borusyak, Hull, and Jaravel (2019), insofar as one is willing to assume cross-sectional heterogeneity in which treatment effects are constant within a location only, then Goldsmith-Pinkham, Sorkin, and Swift (2020) provides some diagnostic aids to help evaluate the plausibility of the design itself.

A second result in Goldsmith-Pinkham, Sorkin, and Swift (2020) is a decomposition of the Bartik estimator into a weighted combination of estimates where each share is an instrument. These weights, called Rotemberg weights, sum to one, and the authors note that higher valued weights indicate that those instruments are responsible for more of the identifying variation in the design itself. These weights provide insight into which of the shares get more weight in the overall estimate, which helps clarify which industry shares should be scrutinized. If regions with high weights pass some basic specification tests, then confidence in the overall identification strategy is more defensible.

7.9 Conclusion

In conclusion, instrumental variables are a powerful design for identifying causal effects when your data suffer from selection on unobservables. But even with that in mind, it has many limitations that have in the contemporary period caused many applied researchers to eschew it. First, it only identifies the LATE under heterogeneous treatment effects, and that may or may not be a policy relevant variable. Its value ultimately depends on how closely the compliers’ average treatment effect resembles that of the other subpopulations. Second, unlike RDD, which has only one main identifying assumption (the continuity assumption), IV has up to five assumptions! Thus, you can immediately see why people find IV estimation less credible—not because it fails to identify a causal effect, but rather because it’s harder and harder to imagine a pure instrument that satisfies all five conditions.

But all this is to say, IV is an important strategy and sometimes the opportunity to use it will come along, and you should be prepared for when that happens by understanding it and how to implement it in practice. And where can the best instruments be found? Angrist and Krueger (2001) note that the best instruments come from in-depth knowledge of the institutional details of some program or intervention. The things you spend your life studying will in time reveal good instruments. Rarely will you find them from simply downloading a new data set, though. Intimate familiarity is how you find instrumental variables, and there is, alas, no shortcut to achieving that.

Causal Inference:
The Mixtape.

Buy the print version today:

Buy from Amazon Buy from Yale Press

Aizer, Anna, and Joseph J. Doyle. 2015. “Juvenile Incarceration, Human Capital, and Future Crime: Evidence from Randomly Assigned Judges.” Quarterly Journal of Economics 130 (2): 759–803.

Angrist, Joshua D. 1990. “Lifetime Earnings and the Vietnam Era Draft Lottery: Evidence from Social Security Administrative Records.” American Economic Review 80 (3): 313–36.

Angrist, Joshua D., Guido W. Imbens, and Alan B. Krueger. 1999. “Jacknnife Instrumental Variables Estimation.” Journal of Applied Econometrics 14: 57–67.

Angrist, Joshua D., Guido W. Imbens, and Donald B. Rubin. 1996. “Identification of Causal Effects Using Instrumental Variables.” Journal of the American Statistical Association 87: 328–36.

Angrist, Joshua D., and Alan B. Krueger. 1991. “Does Compulsory School Attendance Affect Schooling and Earnings?” Quarterly Journal of Economics 106 (4): 979–1014.

———. 2001. “Instrumental Variables and the Search for Identification: From Supply and Demand to Natural Experiments.” Journal of Economic Perspectives 15 (4): 69–85.

Angrist, Joshua D., and Jorn-Steffen Pischke. 2009. Mostly Harmless Econometrics. 1st ed. Princeton University Press.

Arnold, David, Will Dobbie, and Crystal S. Yang. 2018. “Racial Bias in Bail Decisions.” Quarterly Journal of Economics 133 (4): 1885–1932.

Baicker, Katherine, Sarah L. Taubman, Heidi L. Allen, Mira Bernstein, Jonathan Gruber, Joseph Newhouse, Eric Schneider, Bill Wright, Alam Zaslavsky, and Amy Finkelstein. 2013. “The Oregon Experiment – Effects of Medicaid on Clinical Outcomes.” New England Journal of Medicine 368 (May): 1713–22.

Bartik, Timothy J. 1991. Who Benefits from State and Local Economic Development Policies? Kalamazoo, Michigan: W.E. Upjohn Institute for Employment Research.

Becker, Gary. 1994. Human Capital: A Theoretical and Empirical Analysis with Special Reference to Education. 3rd ed. University of Chicago Press.

Blanchard, Olivier Jean, and Lawrence F. Katz. 1992. “Regional Evolutions.” Brookings Papers on Economic Activity 1: 1–75.

Borusyak, Kirill, Peter Hull, and Xavier Jaravel. 2019. “Quasi-Experimental Shift-Share Research Designs.”

Bound, John, David A. Jaeger, and Regina M. Baker. 1995. “Problems with Instrumental Variables Estimation When the Correlation Between the Instruments and the Endogenous Explanatory Variable Is Weak.” Journal of the American Statistical Association 90 (430).

Buckles, Kasey, and Daniel Hungerman. 2013. “Season of Birth and Later Outcomes: Old Questions, New Answers.” Review of Economics and Statistics 95 (3): 711–24.

Card, David. 1995. “Aspects of Labour Economics: Essays in Honour of John Vanderkamp.” In. University of Toronto Press.

Cunningham, Scott, and Keith Finlay. 2012. “Parental Substance Abuse and Foster Care: Evidence from Two Methamphetamine Supply Shocks?” Economic Inquiry 51 (1): 764–82.

Dobbie, Will, Jaconb Goldin, and Crystal S. Yang. 2018. “The Effects of Pretrial Detention on Conviction, Future Crime, and Employment: Evidence from Randomly Assigned Judges.” American Economic Review 108 (2): 201–40.

Dobbie, Will, Paul Goldsmith-Pinkham, and Crystal Yang. 2017. “Consumer Bankruptcy and Financial Health.” Review of Economics and Statistics 99 (5): 853–69.

Dobkin, Carlos, and Nancy Nicosia. 2009. “The War on Drugs: Methamphetamine, Public Health and Crime.” American Economic Review 99 (1): 324–49.

Donald, Stephen G., and Whitney K. Newey. 2001. “Choosing the Number of Instruments.” Econometrica 69 (5): 1161–91.

Doyle, Joseph J. 2007. “Child Protection and Adult Crime: Using Investigator Assignment to Estimate Causal Effects of Foster Care.”

———. 2008. “Child Protection and Child Outcomes: Measuring the Effects of Foster Care.” American Economic Review Forthcoming.

Finkelstein, Amy, Sarah Taubman, Bill Wright, Mira Bernstein, Jonathan Gruber, Joseph P. Newhouse, Heidi Allen, and Katherine Baicker. 2012. “The Oregon Health Insurance Experiment: Evidence from the First Year.” Quarterly Journal of Economics 127 (3): 1057–1106.

Frandsen, Brigham R., Lars J. Lefgren, and Emily C. Leslie. 2019. “Judging Judge Fixed Effects.”

Freeman, Richard B. 1980. “An Empirical Analysis of the Fixed Coefficient ‘Manpower Requirement’ Mode, 1960-1970.” Journal of Human Resources 15 (2): 176–99.

Gaudet, Frederick J., George S. Harris, and Charles W. St. John. 1933. “Individual Differences in the Sentencing Tendencies of Judges.” Journal of Criminal Law and Criminology 23 (5): 811–18.

Gilchrist, Duncan Sheppard, and Emily Glassberg Sands. 2016. “Something to Talk about: Social Spillovers in Movie Consumption.” Journal of Political Economy 124 (5): 1339–82.

Goldsmith-Pinkham, Paul, Isaac Sorkin, and Henry Swift. 2020. “Bartik Instruments: What, When, Why, and How.” American Economic Review Forthcoming.

Graddy, Kathryn. 2006. “The Fulton Fish Market.” Journal of Economic Perspectives 20 (2): 207–20.

Imbens, Guideo W., and Joshua D. Angrist. 1994. “Identification and Estimation of Local Average Treatment Effects.” Econometrica 62 (2): 467–75.

Juhn, Chinhui, Kevin M. Murphy, and Brooks Pierce. 1993. “Wage Inequality and the Rise in Returns to Skill.” Journal of Political Economy 101 (3): 410–42.

Kling, Jeffrey R. 2006. “Incarceration Length, Employment, and Earnings.” American Economic Review 96 (3): 863–76.

Leslie, Emily, and Nolan G. Pope. 2018. “The Unintended Impact of Pretrial Detention on Case Outcomes: Evidence from New York City Arraignments.” Journal of Law and Economics 60 (3): 529–57.

Mueller-Smith, Michael. 2015. “The Criminal and Labor Market Impacts of Incarceration.”

Norris, Samuel, Matthew Pecenco, and Jeffrey Weaver. 2020. “The Effects of Parental and Sibling Incarceration: Evidence from Ohio.”

Perloff, Harvey S. 1957. “Interrelations of State Income and Industrial Structure.” Review of Economics and Statistics 39 (2): 162–71.

Sharpe, Jamie. 2019. “Re-Evaluating the Impact of Immigration on the US Rental Housing Market.” Journal of Urban Economics 111 (C): 14–34.

Staiger, Douglas, and James H. Stock. 1997. “Instrumental Variables Regression with Weak Instruments.” Econometrica 65 (3): 557–86.

Stevenson, Megan T. 2018. “Distortion of Justice: How the Inability to Pay Bail Affects Case Outcomes.” The Journal of Law, Economics and Organization 34 (4): 511–42.

Stigler, Stephen M. 1980. “Stigler’s Law of Eponymy.” Transactions of the New York Academy of Sciences 39: 147–58.

Stock, James H., and Francesco Trebbi. 2003. “Who Invented Instrumental Variable Regression?” The Journal of Economic Perspectives 17 (3): 177–94.

Waldfogel, Joel. 1995. “The Selection Hypotehsis and the Relationship Between Trial and Plaintiff Victory.” Journal of Political Economy 103 (2): 229–60.

---

1. Philip had a passion for poetry, and even published some in his life. He also used his school’s printing press to publish the first book of poems by the great American poet Carl Sandburg.

2. But it’s easy to have the best paper on a topic in some field when you’re also the only paper on that topic in that field.

3. Unobserved ability doesn’t mean it’s literally unobserved, in other words. It could be just missing from your data set, and therefore is unobserved to you.

4. That is, \(S_i = \gamma + \beta Z_i + \epsilon_i\).

5. I wouldn’t go so far as to say that presenting pictures of the reduced form and first stage is mandatory in the way that many pictures in an RDD are mandatory, but it’s awfully close. Ultimately, seeing is believing.

6. I explain the importance of the \(F\) statistic later in this chapter, but ordinarily an \(F\) test on the excludability of the instrument from the first stage is calculated to check for the instrument’s strength.

7. Angrist and Krueger always made such helpful and effective graphics for their studies, and this paper is a great example.

8. I know, I know. No one has ever accused me of being subtle. But it’s an important point—a picture is worth a thousand words. If you can communicate your first stage and reduced form in pictures, you always should, as it will really captivate the reader’s attention and be far more compelling than a simple table of coefficients ever could.

9. Having said that, Buckles and Hungerman (2013) found that in fact there are systematic differences in individual attributes that are predictors of ability by birth quarter!

10. These kinds of falsifications are extremely common in contemporary applied work. This is because many of the identifying assumptions in any research design are simply untestable. And so the burden of proof is on researchers to convince the reader, oftentimes with intuitive and transparent falsification tests.

11. Good luck with that. Seriously, good luck because—and I’m going out on a limb here—if you had a better instrument, you’d be using it!

12. My hunch is economists’ priors assume heterogeneous treatment effects are the rule and constant treatment effects are the exception, but that many others have the opposite priors. It’s actually not obvious to me there is a reason to have any particular priors, but economists’ training tends to start with heterogeneity.

13. Probably no other identifying assumption is given shorter shrift than SUTVA. Rarely is it mentioned in applied studies, let alone taken seriously.

14. We have reviewed the properties of IV with heterogeneous treatment effects using a very simple dummy endogeneous variable, dummy IV, and no additional controls example. The intuition of LATE generalizes to most cases where we have continuous endogenous variables and instruments, and additional control variables, as well.

15. These are funny people. If they’re drafted, they dodge the draft. But if they’re not drafted, then they voluntarily enroll. In this context, defiance seems kind of irrational, but that’s not always the case.

16. These are draft dodgers. For instance, maybe it’s someone whose doctor gave him a bone-spur diagnosis so he could avoid service.

17. These are our patriots.

18. This identification of the LATE under heterogeneous treatment effects material was worked out in Angrist, Imbens, and Rubin (1996).

19. See Emily Leslie’s website https://sites.google.com/view/emilycleslie/home/research to download the Stata ado package.

20. Best name for an estimator ever.

21. Goldsmith-Pinkham, Sorkin, and Swift (2020) note that many instruments have Bartik features. They describe an instrument as “Bartik-like” if it uses the inner product structure of the endogenous variable to construct an instrument.